Оцен­ка вли­я­ния изу­ча­е­мых в экс­пе­ри­мен­те фа­к­то­ров

Ди­с­пер­си­он­ный ана­лиз.

При изу­че­нии свя­зи ме­ж­ду яв­ле­ни­я­ми не­об­хо­ди­мо от­ве­тить на во­п­рос: су­ще­ст­ву­ет ли связь или нет, ка­ко­го по­ряд­ка эта связь (силь­ная или сла­бая), яв­ля­ет­ся ли она свя­зью ме­ж­ду од­ним яв­ле­ни­ем - при­чи­ной и од­ним яв­ле­ни­ем-след­ст­ви­ем, ме­ж­ду не­сколь­ки­ми яв­ле­ни­я­ми-при­чи­на­ми и од­ним яв­ле­ни­ем-след­ст­ви­ем и т.д. Пер­вый из пе­ре­чи­с­лен­ных во­п­ро­сов ре­ша­ет­ся ме­то­дом ди­с­пер­си­он­но­го ана­ли­за. По­лу­ча­ет­ся аль­тер­на­тив­ный с оп­ре­де­лен­ной сте­пе­нью ве­ро­ят­но­сти от­вет на то, су­ще­ст­ву­ет или не су­ще­ст­ву­ет связь ме­ж­ду изу­ча­е­мы­ми яв­ле­ни­я­ми.

Ме­тод ди­с­пер­си­он­но­го ана­ли­за ча­с­то ис­поль­зу­ет­ся при экс­пе­ри­мен­таль­ных ис­сле­до­ва­ни­ях, свя­зан­ных с оцен­кой фа­к­то­ров, ока­зы­ва­ю­щих вли­я­ние на изу­ча­е­мое яв­ле­ние. Су­ще­ст­вен­ную роль при этом иг­ра­ет так на­зы­ва­е­мое срав­не­ние ди­с­пер­сий. Ос­нов­ная идея ме­то­да та­ко­ва.

Ес­ли пред­по­ло­жить, что ис­сле­ду­ет­ся воз­дей­ст­вие не­сколь­ких фа­к­то­ров F1, F2, F3...Fb на при­знак X, ко­то­рым об­ла­да­ют слу­чаи изу­ча­е­мой со­во­куп­но­сти, и что ка­ж­дый фа­к­тор изу­ча­ет­ся m раз, то бу­дет по­лу­че­но bm на­блю­да­е­мых зна­че­ний. При этом воз­мо­ж­но из об­щей ди­с­пер­сии s² всех на­блю­да­е­мых зна­че­ний вы­де­лить ди­с­пер­сию, яв­ля­ю­щу­ю­ся след­ст­ви­ем изу­ча­е­мых фа­к­то­ров - s_f и ди­с­пер­сию, яв­ля­ю­щу­ю­ся след­ст­ви­ем слу­чай­ных при­чин, так на­зы­ва­е­мую ос­та­то­ч­ную ди­с­пер­сию s_e. Срав­ни­вая s_f и s_e мо­ж­но с оп­ре­де­лен­ной сте­пе­нью ве­ро­ят­но­сти ус­та­но­вить, на­сколь­ко су­ще­ст­вен­но дей­ст­вие изу­ча­е­мо­го фа­к­то­ра на ве­ли­чи­ну на­блю­да­е­мо­го при­зна­ка. Даль­ней­шее изу­че­ние ис­сле­ду­е­мых фа­к­то­ров про­во­дят пу­тем срав­не­ния сред­них зна­че­ний на­блю­да­е­мо­го при­зна­ка, по­лу­чен­ных при воз­дей­ст­вии на ка­ж­дый из фа­к­то­ров, при­ме­не­ние ко­то­рых обес­пе­чи­ло наи­бо­лее ва­ж­ные для экс­пе­ри­мен­та­то­ра ре­зуль­та­ты. Ме­то­ду ди­с­пер­си­он­но­го ана­ли­за пред­ше­ст­ву­ет этап по­пар­но­го срав­не­ния сред­них ве­ли­чин. Пре­и­му­ще­ст­во это­го ме­то­да в том, что при его по­мо­щи мо­ж­но в ко­рот­кий срок при ма­лом по объ­е­му на­блю­де­ний изу­чить вли­я­ние мно­гих фа­к­то­ров (или ком­би­на­ций фа­к­то­ров), а за­тем ис­сле­до­вать те из них, дей­ст­вие ко­то­рых обес­пе­чи­ва­ет наи­бо­лее ва­ж­ные ре­зуль­та­ты. В этом от­но­ше­нии ме­тод ди­с­пер­си­он­но­го ана­ли­за яв­ля­ет­ся ме­то­дом срав­не­ния бо­лее чем двух сред­них ве­ли­чин.

Ис­поль­зо­ва­ние ме­то­да ди­с­пер­си­он­но­го ана­ли­за пред­по­ла­га­ет ко­ли­че­ст­вен­ное (а не опи­са­тель­ное) вы­ра­же­ние на­блю­да­е­мых при­зна­ков. Изу­ча­е­мые фа­к­то­ры, од­на­ко, в ча­ст­но­сти их раз­но­вид­но­сти мо­гут быть пред­ста­в­ле­ны как опи­са­тель­но, так и ко­ли­че­ст­вен­но.

Тех­ни­че­с­кие при­е­мы вы­чи­с­ле­ния, ис­поль­зу­е­мые при ди­с­пер­си­он­ном ана­ли­зе и обес­пе­чи­ва­ю­щие оп­ре­де­ле­ние по­ка­за­те­лей об­щей ди­с­пер­сии, ди­с­пер­сии в свя­зи с воз­дей­ст­ви­ем от­дель­ных фа­к­то­ров и ос­та­то­ч­ной ди­с­пер­сии, за­ви­сят от чи­с­ла изу­ча­е­мых фа­к­то­ров и от оди­на­ко­во­го или не­оди­на­ко­во­го чи­с­ла на­блю­де­ний в от­но­ше­нии дей­ст­вия ка­ж­до­го из фа­к­то­ров. В свя­зи с этим раз­ли­ча­ют од­но­фа­к­тор­ный, двух­фа­к­тор­ный и мно­го­фа­к­тор­ный ди­с­пер­си­он­ный ана­лиз; рав­но­мер­ный и не­рав­но­мер­ный ком­п­лекс.

При равномерном комплексе однофакторного дисперсионного анализа изучают действие разновидностей только одного фактора, причем число испытаний каждой разновидности одинаково. Например, изучают влияние нескольких режимов питания на содержание витаминов в организме человека.

Результаты эксперимента равномерного комплекса однофакторного дисперсионного анализа можно представить в виде схемы.

Изучаемый фактор	Повторения
						m
F1	X11	X12	X13	X14	...	X1m
F2	X21	X22	X23	X24	...	X2m
. .	. .	. .	. .	. .	. .	. .
Fb	Xb1	Xb2	Xb3	Xb4	...	Xbm

Первоначально находят общую среднюю по формуле: и средние отдельных факторов по строкам . Используя значения этих средних, находят сумму квадратов отклонений - S=Sd².

Вариация S	Сумма квадратов отклонения Sd^2=S	Число степеней свободы k	Дисперсия s^2	Fф	Ft	Оценка
Общая - S	Sd^2=S= S(X-Xср)^2.	k=bm-1	s^2=S/k	-		-
По факторам		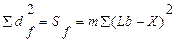k1=b-1	s^2=Sf/k1	s^2f/ s^2e	по таблице	Fф <>Ft
Остаточные	Sd^2e=Se= Sd^2- Sd^2f	k2=mb-b	s^2=Se/k1	-		-

При Fф >=Ft мо­ж­но пред­по­ла­гать, что на­блю­да­е­мое раз­ли­чие су­ще­ст­вен­но. Ес­ли на­обо­рот, то оно слу­чай­но.

При­мер 1. Количество съеденных булочек 8 студентами в течение 6 минут представлено в таблице.

Время	Испытание №	Итог	Средняя Lb
										12,38
										11,13
										8,88
										8,13
										51,52

Необходимо про­ве­рить, дей­ст­ви­тель­но ли в те­че­ние 6 ми­нут ко­ли­че­ст­во съе­ден­ных бу­ло­чек умень­ша­ет­ся или это раз­ли­чие слу­чай­но и яв­ля­ет­ся след­ст­ви­ем ма­ло­го чи­с­ла на­блю­де­ний. Вы­во­ды дол­ж­ны иметь до­ве­ри­тель­ную ве­ро­ят­ность Ft=0.99.

S=(10²+14²+14²+....5²+5²)-(1/8*6)*(10+14+14+....5+5)²=422;

Sf=8*[(12.38²+11.13²+....5²)-1/6(12.38+11.13+....5)²]=300;

Se=422-300=122;

s²=422/(8*6-1)= 8,97;

s_f²=300/(6-1)=60;

s_e²=122/42=3;

Ff=60/3=20;

Ft=3.49;

По­с­ле на­хо­ж­де­ния Ff=20, ос­но­вы­ва­ясь на по­лу­чен­ных ре­зуль­та­тах, с до­с­та­то­ч­но боль­шой ве­ро­ят­но­стью мо­ж­но ут­вер­ждать, что раз­ли­чие су­ще­ст­вен­но и за­ко­но­мер­но.

При не­рав­но­мер­ном ком­п­ле­к­се од­но­фа­к­тор­но­го ди­с­пер­си­он­но­го ана­ли­за изу­ча­ет­ся вли­я­ние раз­но­вид­но­стей толь­ко од­но­го фа­к­то­ра при не­рав­ном чи­с­ле на­блю­де­ний. На­при­мер, экс­пе­ри­мент на­чат по схе­ме рав­но­мер­но­го ком­п­ле­к­са, но по ка­ким-то со­об­ра­же­ни­ям не­ко­то­рые из из­ме­ре­ний при­шлось ус­т­ра­нить, так как они ре­з­ко от­ли­ча­лись от ос­таль­ных. В та­ких слу­ча­ях, для то­го что­бы ис­поль­зо­вать све­де­ния, по­лу­чен­ные при экс­пе­ри­мен­те, при­ме­ня­ют ме­тод од­но­фа­к­тор­но­го ди­с­пер­си­он­но­го ана­ли­за при неравномерном ком­п­ле­к­се.

По­лу­чен­ные при ис­сле­до­ва­нии дан­ные раз­ме­ща­ют­ся в таб­ли­це, ана­ло­ги­ч­ной при­ме­ру 1.

Вре­мя	Ис­пы­та­ние №	Итог	Сред­няя Lb
										11.4
										8,88
										7.5
										5.71

Об­щее чи­с­ло ис­пы­та­ний, од­на­ко, рав­ня­ет­ся не bm, а толь­ко Sm, ко­то­рое все­гда мень­ше. Об­щую ва­ри­а­цию при этой схе­ме ана­ли­за на­хо­дят так­же, как и рань­ше. Ва­ри­а­цию по фа­к­то­рам оп­ре­де­ля­ют по фор­му­ле:

Для ос­та­то­ч­ной ва­ри­а­ции дей­ст­ви­тель­на пре­ды­ду­щая фор­му­ла. Чи­с­ла сте­пе­ней сво­бо­ды рав­ны со­от­вет­ст­вен­но: k=Sm-1; k1=b-1; k2=k*k1:

Ес­ли про­ве­с­ти рас­чет Ff для дан­ной таб­ли­цы, то ока­жет­ся, что раз­ли­чия по прежнему до­с­то­вер­ны 11.54>3.66.

При двух­фа­к­тор­ном ди­с­пер­си­он­ном ана­ли­зе изу­ча­ют воз­дей­ст­вие, ока­зы­ва­е­мое ком­би­на­ци­ей раз­но­вид­но­стей двух фа­к­то­ров на при­зна­ки изу­ча­е­мых яв­ле­ний. При этом не обя­за­тель­но, что­бы раз­но­вид­но­сти изу­ча­е­мых фа­к­то­ров име­ли ко­ли­че­ст­вен­ную оцен­ку - они мо­гут быть пред­ста­в­ле­ны и опи­са­тель­но. По­ста­нов­ка за­да­чи ана­ло­ги­ч­на опи­сан­ной в пре­ды­ду­щих при­ме­рах. По­лу­чен­ные ре­зуль­та­ты рас­сма­т­ри­ва­ют как об­щую вы­бор­ку, в ко­то­рой не­сколь­ко (чи­с­лен­но­стью a*b) под­вы­бо­рок.

За­да­ча, ко­то­рую на­до ре­шить сле­ду­ю­щая: мо­ж­но ли счи­тать, что та­ко­го ро­да вы­бор­ка взя­та из од­ной и той же ге­не­раль­ной со­во­куп­но­сти, или пра­виль­нее счи­тать, что от­дель­ные под­вы­бор­ки от­но­сят­ся к раз­ли­ч­ным ге­не­раль­ным со­во­куп­но­стям? Например, изучается воздействие, оказываемое комбинацией двух факторов: Fa - минута приема пищи и Fb - способ лечения студентов от обжорства на количество съеденных булочек. У фактора Fa - a разновидностей, а у фактора Fb - b разновидностей. Число подвыборок в этом случае будет равно произведению a*b. В каждой подвыборке изучают равное число случаев - m. Следовательно общее число случаев равно a*b*m. При такой постановке исследования можно ответить на следующие вопросы: существенно ли раздельное влияние факторов Fa и Fb на количество съеденных плюшек и существенно ли комбинированное влияние, оказываемое обоими факторами. Ответ на этот вопрос получают, определив, сформированы ли отдельные подвыборки из состава одной и той же генеральной совокупности или нет. Для этого используют таблицу в которой представлена схема двухфакторного анализа (Сепетлиев Д. Статистические методы в научных медицинских исследованиях. М. Медицина. 1968. с158-175).

Дата добавления: 2014-01-05