Статистические ряды распределения

В группах проведем статистическую сводку показателей

Таблица 2.6

Группировка предприятий одного из регионов России по выпуску продукции

(структурная группировка)

№ группы	Группы предприятий по выпуску продукции, млн руб.	Число предприятий, ед.	Выпуск продукции	Прибыль
всего, млн руб.	в % к итогу	всего, млн руб.	в % к итогу
	41–61 61–81 81–101			16,9 53,5 29,6	97,0 259,7 126,4	20,1 53,8 26,2
	Итого			100,0	483,1	100,0

По данным структурной группировки предприятий можно сделать вывод, что наибольший удельный вес выпуска и прибыли приходится на предприятия 2-й группы.

Таблица 2.7

Группировка предприятий одного из регионов России по выпуску продукции

(аналитическая группировка)

№ группы	Группы предприятий по выпуску продукции, млн руб.	Число предприятий, ед.	Выпуск продукции, млн руб.	Прибыль, млн руб.
всего	в среднем на 1 пред-приятие	всего	в среднем на 1 пред-приятие
	41–61 61–81 81–101			50,9 70,6 89,4	97,0 259,7 126,4	13,9 16,2 18,1
	Итого			70,4	483,1	16,1

В данной совокупности предприятий средний выпуск продукции в расчете на 1 предприятие составил 70,4 млн руб., прибыли – 16,1 млн руб. С увеличением выпуска продукции средние значения прибыли увеличиваются. Так, в третьей группе по сравнению с первой выпуск продукции, приходящийся на 1 предприятие, выше на 38,5 млн руб., а прибыль – выше на 4,2 млн руб. Если выпуск продукции увеличится на 1 млн руб., то прибыль увеличится на 0,11 млн руб. (4,2/38,5 = 0,11).

Статистический ряд распределения – это упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.

Любой ряд распределения состоит из двух элементов: вариантов и частот.

Вариант (x) – отдельное значение признака, которое он принимает в ряду распределения.

Частота (f) – это количество единиц совокупности, которые принимают данное значение признака.

Выделяют:

– атрибутивные ряды распределения, построенные по качественному признаку;

– вариационные ряды распределения, построенные по количественному признаку.

В зависимости от характера признака различают дискретные и интервальные вариационные ряды.

В дискретном вариационном ряду распределения варианты признака задаются конкретными числами.

В интервальном вариационном ряду распределения варианты признака задаются интервалом.

Дискретные ряды распределения графически изображаются в виде полигона распределения.

Пример: дан следующий дискретный ряд распределения.

Таблица 2.8

Распределение семей по числу детей

Группы семей по числу детей, чел.	Количество семей, ед.
Итого

Изобразите ряд графически.

Подпись: число семей, ед.(

Иногда на оси ординат вместо частот (f) отмечают частости – это частоты, выраженные в процентах к общему числу единиц совокупности.

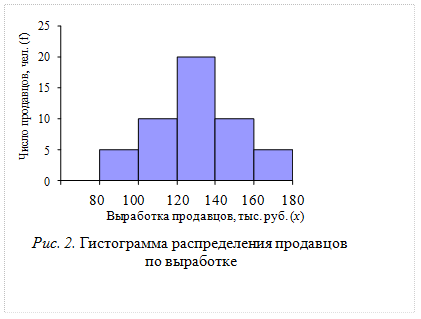
Интервальные ряды распределения графически изображаются с помощью гистограммы и кумуляты распределения.

Пример: задан интервальный ряд распределения.

Таблица 2.9

Распределение продавцов магазина по выработке

Выработка продавцов, тыс. руб. (х)	Число продавцов, чел. (f)	Частость, % (число продавцов в % к итогу)	Кумулятивная (накопленная) частота, чел. (S)
80-100
100-120
120-140
140-160
160-180
Итого			Х

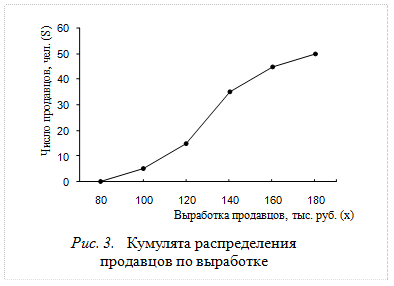
Изобразите ряд графически (см. рис. 2 и рис. 3).

Ряд распределения, состоящий из двух граф (варианты и частоты), иногда дополняется другими графами, необходимыми для вычисления отдельных статистических показателей или для более отчетливого выражения характера вариации изучаемого признака. Достаточно часто в ряд вводится графа, в которой подсчитываются накопленные частоты (S). Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем данное значение, и исчисляются путем последовательного прибавления к частоте первого интервала частот последующих интервалов (см. пример расчета в последней графе табл. 2.9).

Частоты ряда (f) могут быть заменены частостями (w), которые представляют собой частоты, выраженные в относительных числах (долях или процентах) и рассчитанные путем деления частоты каждого интервала на их общую сумму (см. пример расчета в третьей графе табл. 2.9). Замена частот частостями позволяет сопоставлять вариационные ряды с различным числом наблюдений.

Если вариационный ряд дан с неравными интервалами, то для правильного представления о характере распределения необходимо произвести расчет абсолютной или относительной плотности распределения. Тогда на оси ординат при построении гистограммы вместо частот (частостей) отмечают плотность распределения.

Абсолютная плотность распределения – это частота, рассчитанная на единицу длины интервала, т. е. сколько единиц в каждой группе приходится на единицу длины интервала.

Относительная плотность распределения – частное от деления частости отдельной группы на размер ее интервала.

Эти показатели используются для преобразования интервалов, что бывает необходимо при сравнительной оценке двух группировок.

Дата добавления: 2014-01-05