Средняя арифметическая

Есть частное от деления суммы всех значений признака на их число. Применяется в тех случаях, когда объем варьирующего признака для всей совокупности образуется как сумма значений признака у отдельных единиц. Например, общий фонд заработной платы – это сумма заработных плат всех работников.

Частные случаи расчета средней арифметической

1) Средняя арифметическая по данным вариационного ряда:

а) средняя арифметическая по данным дискретного вариационного ряда распределения:

Пример 1:

Таблица 5.2

Распределение семей по числу детей

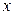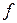
Группы семей по числу детей, чел. ()	Число семей, ед.	Число детей
Итого

Определите среднее число детей в семье.

Решение:

Решение любой задачи на определение средней начинаем с записи исходного соотношения средней (ИСС), т. е. формулы, по которой определяется среднее значение признака.

ИСС:

Совокупное число детей во всех семьях

Среднее число детей в семье = –––––––––––––––––––––––––––––––––––– =

Количество семей

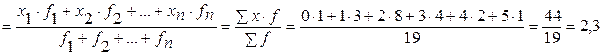чел.

Ответ: среднее число детей в семье 2,3 человека. Для расчета использовали формулу средней арифметической взвешенной.

б) средняя арифметическая в интервальном вариационном ряду распределения:

При расчете среднего значения признака по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам и расчет производят аналогично дискретному ряду распределения.

Пример 2:

Таблица 5.3

Распределение рабочих по размеру заработной платы в месяц

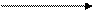Группы рабочих по размеру заработной платы в месяц, руб. (х)	Среднее значение интервала, руб. (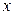)	Число рабочих, чел. (Частота 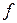)	Общий фонд заработной платы, руб., ()
10000 – 15000 15000 – 20000 20000 – 25000 25000 – 30000			125 000 875 000 900 000 550 000
Итого	х

Определите среднюю заработную плату рабочих.

Решение:

Исходное соотношение средней:

Фонд заработной платы

Средняя заработная плата = –––––––––––––––––––––– =

Количество рабочих

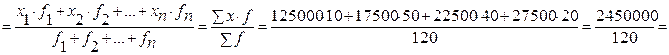
= 20417 руб.

Ответ: средняя заработная плата работников предприятия равна 20417 руб.

2) Частным случаем средней арифметической является средняяхронологическая, которая применяется для расчета среднего значения по данным моментного ряда динамики.

Формула средней хронологической:

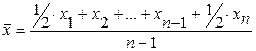
Пример 3:

Остатки товаров составили, тыс. руб.: на 1.01 500

на 1.02 550

на 1.03 530

на 1.04 520

Определить средний остаток товаров за I квартал.

Решение:

Можно вычислять по формуле средней арифметической простой.

Исходное соотношение средней:

cр. остаток за янв. + ср. ост. за февр.+ ср. ост. за март

cр. ост. товара за I кв. = ––––––––––––––––––––––––––––––––––––––––––––––––– =

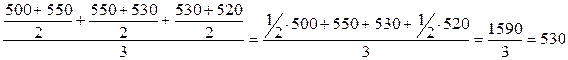=тыс. руб.

Или сразу по формуле средней хронологической:

тыс. руб.

Ответ: средний остаток товара за I квартал равен 530 тыс. руб.

Дата добавления: 2014-01-05