Средняя форма индекса

Средняя форма индексов применяется в тех случаях, когда невозможно определить индексы по агрегатной форме из-за отсутствия какой-либо информации.

Например, нужно рассчитать общий индекс цен. Выписываем его агрегатную формулу:

.

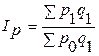Пусть в условии задачи не известны цены базисного периода (р₀), но заданы индивидуальные индексы цен (i_p). Тогда из формулы индивидуального индекса цен выражаем р₀:

.

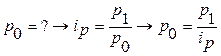Полученное выражение для р₀ подставляем в агрегатную формулу индекса цен:

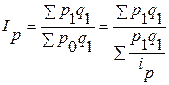– средний гармонический индекс цен.

Пусть теперь нужно рассчитать общий индекс физического объема. Выписываем его агрегатную формулу:

.

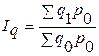Предположим, в этой формуле не известны количества товара в отчетном периоде (q₁), но известны индивидуальные индексы физического объема (i_p). Из формулы индивидуального индекса физического объема выражаем q₁:

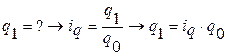
и подставляем это выражение в агрегатную формулу индекса:

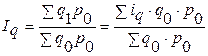– средний арифметический индекс физического объема.

Пример 1: Имеются следующие данные о продаже молочных продуктов на городском рынке:

Таблица 7.2

Данные о продаже молочных продуктов на городском рынке

Продукт	Товарооборот, тыс. руб.	Изменение цены в феврале по сравнению с январем, %
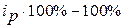
Январь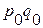	Февраль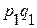
Сметана Молоко Творог	5,5 7,5 9,0	8,7 7,2 10,4	+4,5 +3,1 –2,0

Рассчитайте сводные индексы цен, товарооборота и физического объема продаж. Определите изменение товарооборота за счет действия различных факторов.

Решение:

1) Введем в табл. 7.2 обозначения:

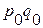· – это товарооборот января (январь базисный период);

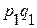· – товарооборот февраля (февраль отчетный период);

· изменение цен в феврале по сравнению с январем по каждому товару в процентах характеризуют индивидуальные индексы цен (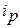), чтобы определить, на сколько процентов изменились цены, нужно из индекса цен вычесть 100%: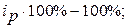

2) Рассчитаем сводный (общий) индекс цен.

Выписываем его агрегатную формулу: 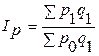. Значения 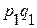для каждого товара известны, поэтому числитель индекса определить можем, а вот знаменатель нет. Выразим 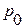для каждого товара из формул :

.

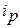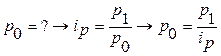Полученное выражение для р₀ подставляем в агрегатную формулу индекса цен:

.

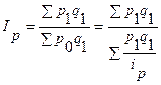Рассчитаем индивидуальные индексы цен:

для сметаны 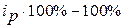=+4,5%, значит 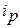=1,045;

для молока 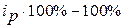=+3,1%, значит 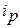=1,031;

для творога 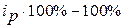=-2,0%, значит 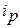=0,98.

Подставляем полученные числовые значения в формулу индекса цен:

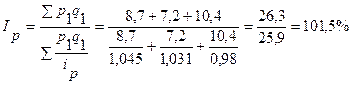, т. е. цены на данную группу молочных товаров в феврале по сравнению с январем увеличились на 1,5%;

3) Рассчитаем общий индекс товарооборота:

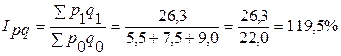, т. е. товарооборот в феврале по сравнению с январем увеличился на 19,5%;

4) Рассчитаем общий индекс физического объема:

, т. е. физический объем продаж молочных товаров на рынке города увеличился на 17,7%;

5) Определим изменение товарооборота за счет действия различных факторов:

– за счет изменения цен:

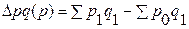=26,3 – 25,9 = 0,4 тыс. руб., т. е. за счет увеличения цен в феврале по сравнению с январем товарооборот увеличился на 0,4 тыс. руб., или на 1,5% (см. 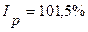) – это величина перерасхода покупателей за счет увеличения цен;

– за счет изменения физического объема продаж:

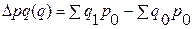= 25,9 – 22,0 = 3,9 тыс. руб., т. е. за счет увеличения физического объема продаж товарооборот увеличился на 3,9 тыс. руб., или на 17,7% (см. 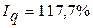) – это выигрыш потребителей за счет увеличения объема потребления;

– в целом:

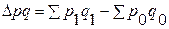=26,3 – 22,0 = 4,3 тыс. руб., т. е. в целом товарооборот увеличился на 4,3 тыс. руб., или на 19,5% (см. ).

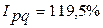Должны выполняться следующие равенства:

1) ;

.

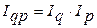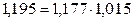2) ;

.

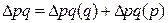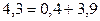III. В зависимости от выбора базы сравнения:

1) ряды индексов с переменной базой сравнения – цепные индексы. В системе цепных индексов уровни индексируемого показателя сопоставляются с уровнями предыдущих периодов;

2) ряды индексов с постоянной базой сравнения – базисные индексы. В системе базисных индексов сравнение уровней индексируемого показателя в каждом индексе производят с уровнем базисного периода.

Цепные и базисные индексы могут быть как индивидуальными так и общими.

Для индивидуальных цепных и базисных индексов выполняется следующая взаимосвязь:

1) произведение всех последовательных цепных индексов дает базисный индекс за рассматриваемый период (последний базисный);

2) частное от деления данного базисного индекса на предыдущий равно цепному.

IV. В зависимости от выбора весов цепных и базисных индексов:

1) индексы с постоянными весами;

2) индексы с переменными весами.

Система индексов с постоянными весами – это система индексов одного и того же явления, вычисленных с весами, не меняющимися при переходе от одного индекса к другому:

а) система базисных индексов с постоянными весами:

; ;

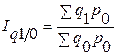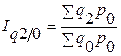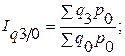
б) система цепных индексов с постоянными весами:

; ;

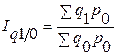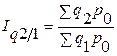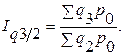
Система индексов с переменными весами – это система индексов одного и того же явления, вычисленных с весами, последовательно меняющимися при переходе от одного индекса к другому:

а) система базисных индексов с переменными весами:

; ;

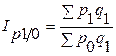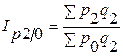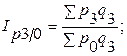
б) система цепных индексов с переменными весами:

; ;

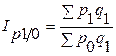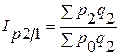Ряды агрегатных индексов с постоянными весами имеют преимущества: сохраняется взаимосвязь между цепными и базисными индексами. Таким образом, использование постоянных весов в течение ряда лет позволяет переходить от цепных общих индексов к базисным, и наоборот.

В рядах агрегатных индексов с переменными весами умножение цепных индексов не дает базисных. Для таких индексов переход от цепных индексов к базисным и наоборот невозможен. Вместе с тем в статистической практике часто возникает необходимость определения динамики цен за длительный период времени на основе цепных индексов цен с переменными весами. Тогда для получения приближенного значения базисного индекса цепные индексы цен перемножают, заведомо зная, что в таком расчете допускаются ошибки.

Дата добавления: 2014-01-05