Основные способы формирования выборочной совокупности

1) Собственно-случайный. Отбор единиц из генеральной совокупности производится в случайном порядке. Случайность отбора заключается в соблюдении 1-го принципа. На практике применяется жеребьевка или таблица случайных чисел.

Все виды выборок производятся по схеме повторного и бесповторного отбора. При повторном отборе, отобранная из генеральной совокупности единица после её регистрации, возвращается в генеральную совокупность и имеет возможность снова попасть в выборку. При бесповторном отборе отобранная единица не возвращается в генеральную совокупность, т. е. не имеет возможности снова попасть в выборку, а оставшиеся единицы имеют большую возможность попасть в выборку, что нарушает первый принцип.

Для устранения указанного недостатка в подкоренное выражение формулы средней ошибки выборки вводится поправочный коэффициент :

.

Иногда на практике пользуются формулами без поправочного коэффициента, хотя выборку организуют как бесповторную, например, когда N неизвестно или безгранично, n очень мало по сравнению с N.

Для более точных расчетов необходимо проводить повторный отбор, но это не всегда возможно, поэтому используется бесповторный.

2) Механический. Отбор единиц в выборочную совокупность из генеральной, разбитой по нейтральному признаку на равные интервалы или группы, производится таким образом, чтобы из каждой такой группы в выборку попала лишь одна единица. Чтобы избежать систематической ошибки, отбираться должна единица, находящаяся в середине каждой группы. При организации механического отбора единицы совокупности располагают в определенном порядке, после чего отбирают заданное число единиц механически через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки. Так при 2%-й выборке отбирается и проверяется каждая 50-я единица (1:0,02), при 5%-м отборе – каждая 20-я (1:0,05). При достаточно большой совокупности механический отбор по точности результатов близок к собственно-случайному, поэтому для определения средней ошибки механической выборки используют формулы собственно-случайной бесповторной выборки.

3) Типологический. Типологическая выборка применяется для отбора единиц из неоднородной совокупности. Единицы генеральной совокупности предварительно объединяются по какому-либо типическому признаку в группы и отбор проводится в пределах этих групп.

Пример: разделим Кировскую область по характеру природных условий на три зоны:

– северная 300 предприятий;

– центральная 500 предприятий;

– южная 200 предприятий.

Из всех предприятий следует сформировать 10%-ю выборку (численность выборки составит 100 предприятий): (300 + 500 + 200)·0,1 = 100 предприятий.

Отбор из каждой группы в выборку возможен по следующим схемам:

1) равномерный отбор (равное число единиц из каждой группы);

2) пропорционально среднему квадратическому отклонению в группах;

3) пропорционально численности единиц в группах;

4) пропорционально среднему квадратическому отклонению в группах и численности групп.

На практике чаще применяется отбор пропорционально численности единиц в группах. Более точный – последний.

Типическая выборка дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представительство в ней каждой типической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки, поэтому при определении средней ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.

4) Серийный. Когда единицы располагаются сериями, отбирать отдельные единицы нецелесообразно, проще организовать отбор серий и провести сплошное обследование выборки. Поскольку внутри серий обследуются все без исключения единицы, средняя ошибка выборки (при отборе равновеликих серий) зависит только от межгрупповой или межсерийной дисперсии.

5) Комбинированный. Перечисленные способы отбора в практике в чистом виде используются редко, чаще сочетаются, этот способ более точен.

Таблица 8. 3

Формулы расчета средней ошибки выборки μ

Способ отбора	Для средней	Для доли
Собственно-случайный повторный
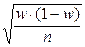
Случайный и механический бесповторный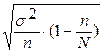
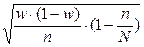
Типологический бесповторный
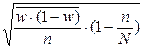
Серийный бесповторный с равновеликими сериями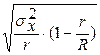

где 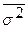– средняя из выборочных дисперсий типических групп;

– средняя дисперсия доли признака в выборочной совокупности;

r – число серий в выборочной совокупности;

R – число серий в генеральной совокупности;

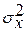– межсерийная дисперсия средних;

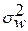– межсерийная дисперсия доли.

Пример 1: При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате установлен средний вес изделий – 30 грамм, при среднем квадратическом отклонении – 4 грамма. С вероятностью 0,997 определите пределы, в которых находится средний вес изделий в генеральной совокупности.

Дано: n = 200 изделий г г P = 0,997 Найти:

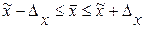
Решение: для определения интервала среднего веса изделий в генеральной совокупности необходимо знать величину предельной ошибки выборки, которая определяется по формуле: 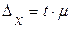. Так как по условию задачи вероятность Р = 0,997, то по табл. 8.2 ей соответствует следующее значение коэффициента доверия: t = 3. Был произведен случайный повторный отбор, по табл. 8.3 выбираем формулу для расчета средней ошибки выборки: 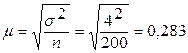г. 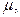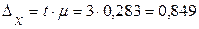Зная t и определим величину предельной ошибки выборки: г. Тогда интервал среднего веса изделий в генеральной совокупности будет таким: ; ; .

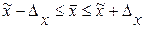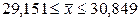Ответ: с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,151 г до 30,849 г.

Дата добавления: 2014-01-05