Гармонический баланс

Рассмотрим известную структуру нелинейной системы

W(jw)

W_H(A)

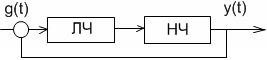
Характеристическое уравнение в данной системе

1+W(jw) * W_H(A)=0

Переходя в показательную форму и выносив за знак равенства единицу получим выражение:

1 * е^-j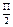=A(w)e^jφ(w) * J(A) e^jµ(A)

L=√-1²+0²=1

α= arctg-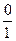=-arctg∞=-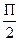

z=Le^-jα=1 * е^-j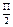

1 * е^-j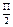= A(w) * J(A) e^jµ(A) e^jφ(w)

Запишем амплитуду и фазу выражения отдельно и получим:

1= A(w) * J(A)

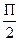-=φ(w)+µ(A)

A(w) =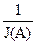

φ(w)= -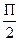- µ(A)

Видно в левой части АЧХ и ФЧХ линейной части. В правой части обратная амплитудная характеристика нелинейной части и фазовая характеристика нелинейной части. Логарифмируя первую часть и умножая ее на 20, получаем систему уравнений:

20 lg A(w) =20 lg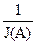

φ(w)= -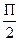- µ(A)

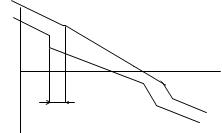
Графическое решение этой системы уравнения будет выглядеть в виде точек пересечения характеристик, и на горизонтальной оси можно будет наблюдать частоту и амплитуду возникающих автоколебаний. При анализе НСАР характеристики нелинейных систем принято представлять в шаблонах и анализ ввести путем наложения получим:

L

20 lg

20 lg A(w)

w(A)

φ(w)

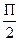-- µ(A)
ИССЛЕДОВАНИЕ И СИНТЕЗ ДВУХКОНТУРНОЙ НЕЛИНЕЙНОЙ 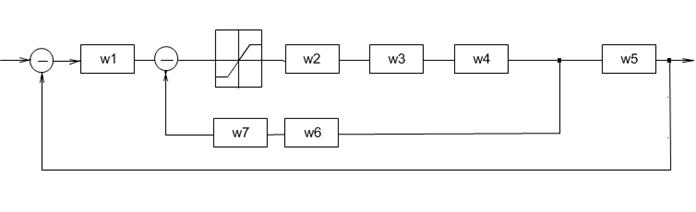САР

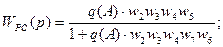
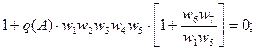
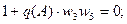
Несмотря на то, что система была многоконтурной, характеристическое уравнение можно свести к аналогичному, в случае одноконтурной системы. Далее можно использовать все методы исследования одноконтурных систем.

СИНТЕЗ (СИСТЕМА) НЕЛИНЕЙНЫХ САР

Основными свойствами нелинейных САР является возникновение автоколебаний. Остальные свойства, такие как точность, запас устойчивости, качество, больше зависят от линейной части системы и при синтезе нелинейных САР необходимо иметь в виду 2 основных момента:

1) Коррекция линейной части системы

2) Подавление автоколебаний

1) коррекция САР проводится по известному нам методу

2) Подавление автоколебаний с помощью введения линейных и нелинейных звеньев.

Наиболее подходящей является коррекция с помощью линейных звеньев. Мы можем синтезировать линейную часть САР в соответствии с предъявляемыми критериями качества, а так же можем подавить возникающие автоколебания изменением характеристики нелинейной части системы.

Дата добавления: 2014-01-05