АФЧХ импульсных систем

Передаточная функция для импульсной САР имеет вид:

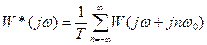
Как видно, характеристика для импульсных САР состоит из бесконечного количества составляющих

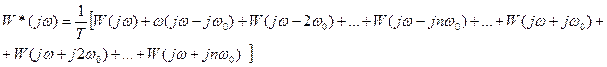
Учитывая инерционность линейной части системы при анализе с помощью АФЧХ можно учитывать несколько первых слагаемых ряда. Для каждого из слагаемых необходимо построить отдельные АФЧХ и результирующая АФЧХ будет находиться как сумма векторов, образующих элементарные характеристики. Выделим 2 первых слагаемых ряда:

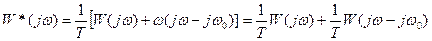
Каждая из этих составляющих представляет собой АФЧХ, т.е каждое можно представить в виде комплексного выражения и по нему построить кривую.

Предполагается, что импульсная система состоит из линейных частей, соответственно импульсы будут фильтроваться и при достаточной их инерционности можно рассматривать первые несколько членов ряда.

Ранее рассматривалось построение АФЧХ по точкам, в нашем случае удобно пользоваться показательной формой записи комплексных выражений.

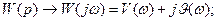
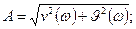
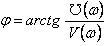
Тогда АФЧХ можно представить так:

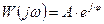
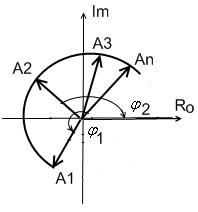АФЧХ получится в результате перемещения некоторого вектора, вычерчиваясь его концом.

Рассмотрим построение АФЧХ для импульсной САР, для этого выберем два члена ряда К=0 и К=-1

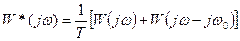
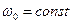
Изменяя частоту 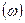от 0 до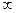

Складывая векторы при определенных значениях частот, получаем результирующую характеристику.

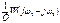
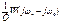
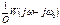
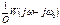
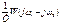
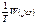
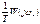
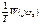
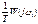
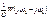
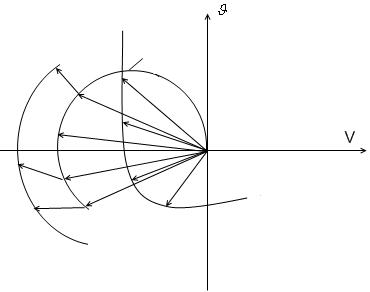
Как видно из характеристики, устойчивость будет тем выше, чем выше фильтрующие способности линейной части. Т.к. при этом результирующая АФЧХ становится ближе началу координатных осей и дальше от точки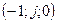

Частота дискретизации отвечает за состояние между АФЧХ.

Пример:

Построение АФЧХ системы

;

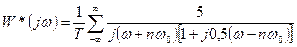Построить АФЧХ при 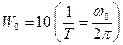при n=0 и n=-1.

При n=0:

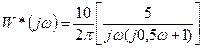
При n=-1:

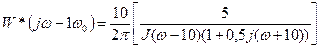
Для каждого из этих выражений определяем мнимую вещественную часть и строят АФЧХ вышеописанным образом.

Дата добавления: 2014-01-05