Ошибки выборочного наблюдения. Предельная теорема, предельная ошибка

Между признаками выборочной совокупности и генеральной совокупности, как правило, существует некоторое расхождение, которое называется ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин:

1) ошибки регистрации или технические ошибки связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т.п;

2) под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и разыскиваемой истинной характеристикой генеральной совокупности:

а) систематические ошибки связаны с нарушением установленных правил отбора;

б) случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности.

В результате систематической ошибки выборка легко может оказаться смещенной, т.к. при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, являясь постоянной частью ошибки репрезентативности, она увеличивается с увеличением объема выборки. Размер ошибки смещения определить очень сложно, иногда невозможно.

Ошибки смещения бывают преднамеренные и непреднамеренные. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появления такой ошибки, необходимо соблюдать принцип случайности отбора единиц. Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появления таких ошибок, необходима хорошая основа выборки.

Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности; с увеличением объёма выборки случайная ошибка уменьшается. Теоретическим обоснованием работы со случайными ошибками выборки является теория вероятностей и ее предельные теоремы.

Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая. Поскольку случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала.

Предельные теоремы теории вероятностей позволяют определять размер случайных ошибок выборки. Различают среднюю (стандартную) и предельную ошибку выборки. Под средней (стандартной) ошибкой выборки понимают такое расхождение между средней выборочной и генеральной совокупностью (), которое не превышает ±Δ. Предельной ошибкой выборочного наблюдения называется разность между величиной средней в генеральной совокупности и ее величиной, вычисленной по результатам выборочного наблюдения (5.1):

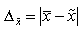. (5.1)

В курсах математической статистики доказано, что величина предельной ошибки выборки не должна превышать соотношения (5.2):

, (5.2)

где величина μ называется средней ошибкой выборки ив общем виде определяется по формулам (5.3) или (5.4):

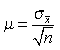, (5.3)

μ = 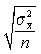. (5.4)

где — среднее квадратическое отклонение в генеральной совокупности;

n — число наблюдений.

В качестве предельной ошибки обычно рассматривается произведение средней ошибки выборки и коэффициента доверия t - параметра, указывающего на конкретное значение вероятности того, на какую величину генеральная средняя будет отличаться от выборочной средней.

Соотношение между дисперсиями генеральной и выборочной совокупности при этом выражается формулой (5.5):

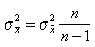. (5.5)

Случайный отбор может быть бесповторным и повторным. При бесповторном отборе единица, попавшая в выборочную совокупность, обратно в генеральную не возвращается. Следовательно, численность генеральной совокупности всё время уменьшается (по такой схеме проходят, например, тиражи различных лотерей). При повторном отборе отобранная единица наблюдения возвращается в генеральную совокупность обратно. Таким образом, численность генеральной совокупности в процессе проведения выборочного обследования остается все время неизменной.

Расчет средней ошибки повторной случайной выборки:

1) cредняя ошибка для средней (5.3) или (5.4);

2) cредняя ошибка для доли 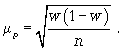(5.6):

(5.6)

Расчет средней ошибки бесповторной случайной выборки:

1) средняя ошибка для средней 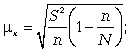(5.7):

(5.7)

2) средняя ошибка для доли 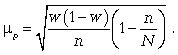(5.8):

(5.8)

Расчет предельной ошибки повторной случайной выборки:

1) предельная ошибка для средней (теорема Чебышева—Ляпунова—Лапласа) 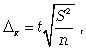(5.9):

(5.9)

2) предельная ошибка для доли (5.10):

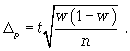(5.10)

Расчет предельной ошибки бесповторной случайной выборки:

1) предельная ошибка для средней (5.11):

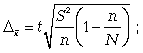(5.11)

2) предельная ошибка для доли (5.12):

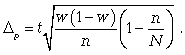(5.12)

Дата добавления: 2014-01-05