
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчет неразветвленной магнитной цепи
|
|
|
|
Расчет магнитных цепей
Расчет магнитных цепей сводится к двум задачам:
1. Прямая задача
Известны:  или
или 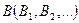
Определить: м.д.с.  или м.д.с. постоянного магнита.
или м.д.с. постоянного магнита.
2. Обратная задача
Известны: м.д.с. 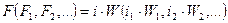
Определить:  или
или 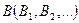
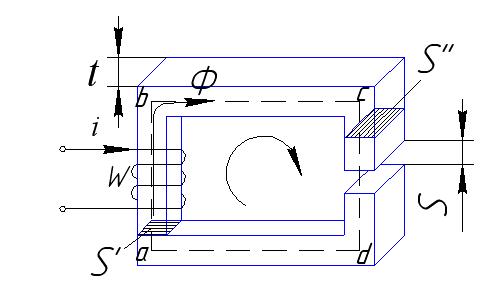
Геометрия:
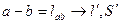
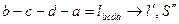
1. Прямая задача
Известно: 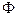
Найти: 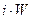
Решение:
Запишем уравнения по 2 закону Кирхгофа:
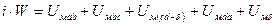 (52)
(52)
Здесь магнитный поток один и тот же.
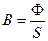
В данной цепи два сечения, следовательно:
 и
и 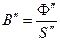
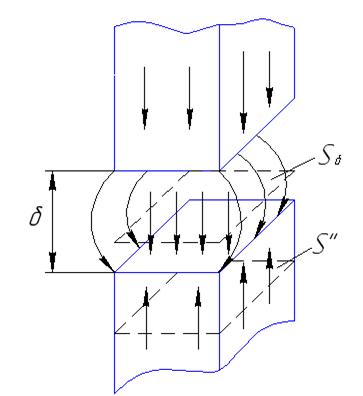
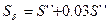
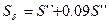
Обычно зазоры относительно ширины магнитопровода небольшие, поэтому принимают  . Следовательно:
. Следовательно:
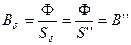
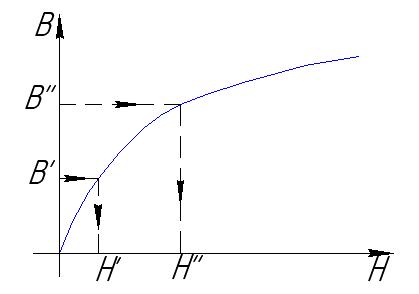 По кривой намагничивания магнитопровода определяем
По кривой намагничивания магнитопровода определяем 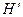 и
и 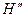 .
.
Кривая намагничивания обычно задается в табличной форме.
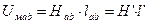
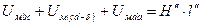 , где
, где 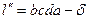
Здесь в воздушном зазоре:  .
.
Так как 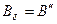 , то
, то 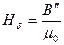 , где
, где  .
.
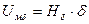
Таким образом, уравнение (52) запишется в виде:
 (53)
(53)
Напряженности найдены, размеры участков известны. Следовательно, 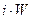 найдено.
найдено.
2. Обратная задача
Известно: м.д.с. (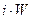 )
)
Найти: 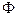
Решение:
Запишем уравнения по 2 закону Кирхгофа в соответствии с геометрией:
 , где
, где  ,
, 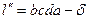
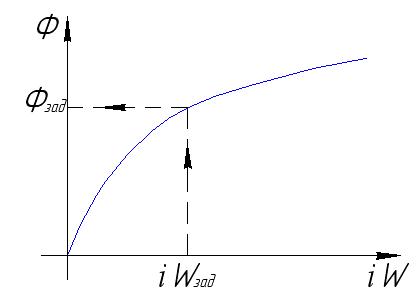
Будем решать задачу графоаналитическим методом.
Необходимо построить зависимость 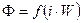 . Для построения составляем таблицу в соответствии с геометрией нашей цепи.
. Для построения составляем таблицу в соответствии с геометрией нашей цепи.
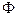
| 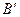
| 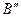
| 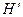
| 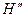
| 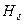
| 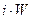
|
 0 0
|  
| 
 0 0
| ||||
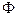
| 0,2 | 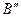
| 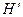
| 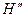
| 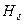
| 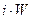
|
| … | … | … | … | … | … | … |
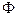
| 1,8 | 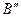
| 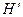
| 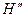
| 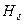
| 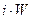
|
Схема решения следующая: задаемся значениями магнитного потока, и определяются соответствующие значения магнитной индукции и напряженности. По уравнению (53) определяется 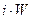 .
.
Так как диапазон изменения магнитного потока трудно оценить, то обычно задаются значениями магнитной индукции 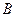 в стержне с минимальным сечением. Известно, что магнитная индукция изменяется в диапазоне:
в стержне с минимальным сечением. Известно, что магнитная индукция изменяется в диапазоне: 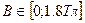 . Выбираем шаг 0,2 Тл.
. Выбираем шаг 0,2 Тл.
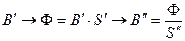
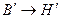
 по кривой намагничивания
по кривой намагничивания
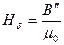
 Подставляя найденные значения в уравнение (53), находят
Подставляя найденные значения в уравнение (53), находят 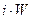 .
.
 Расчет разветвленной магнитной цепи
Расчет разветвленной магнитной цепи
1 стержень 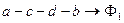
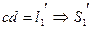
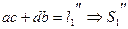
2 стержень 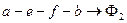
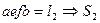
3 стержень 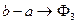
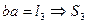
1. Прямая задача
Известны: 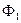 и
и 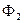
Найти: 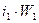 ,
, 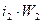
Решение:
Запишем уравнения по законам Кирхгофа для магнитной цепи:
b)  (54)
(54)
I)  (55)
(55)
II) 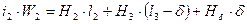 (56)
(56)
1) Находим поток 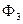 из уравнения (54).
из уравнения (54).
2) Находим магнитные индукции 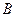 на всех участках:
на всех участках:
 ;
; 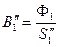 ;
;  ;
; 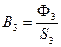
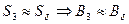
3)  Находим напряженности
Находим напряженности  на всех участках по кривой намагничивания:
на всех участках по кривой намагничивания:
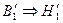
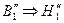
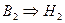
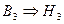
 , где
, где  .
.
4) Подставляя найденные значения напряженностей  в уравнения (55) и (56), находим м.д.с.
в уравнения (55) и (56), находим м.д.с. 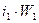 ,
, 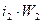 .
.
2. Обратная задача
Известно: 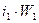 и
и 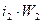 .
.
Найти: 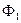 ,
, 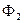 ,
, 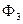 .
.
Решение:
Запишем уравнения по законам Кирхгофа для магнитной цепи:
b)  (57)
(57)
I)  (58)
(58)
II) 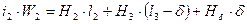 (59)
(59)
При рассмотрении обратной задачи для неразветвленной магнитной цепи строилась зависимость 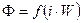 ,и по известным
,и по известным 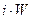 находился соответствующий магнитный поток
находился соответствующий магнитный поток  .
.
В данной задаче три магнитных потока и две м.д.с. Для графоаналитического решения ее необходимо построить зависимость магнитных потоков, как функции от одного общего аргумента. Очевидно, что в данной схеме удобно выбрать общим аргументом падение магнитного напряжения на участке ba - 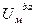 .
.
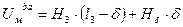 (60)
(60)
Подставив выражение (60) в уравнение (58), получим:
 (61)
(61)
В этом уравнении все параметры связаны с магнитным потоком 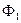 , поэтому по этому уравнению построим зависимость
, поэтому по этому уравнению построим зависимость  .
.
Подставив выражение (60) в уравнение (59), получим:
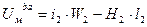 (62)
(62)
В этом уравнении все параметры связаны с магнитным потоком 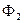 , поэтому по этому уравнению построим зависимость
, поэтому по этому уравнению построим зависимость 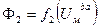 .
.
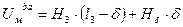
Здесь все параметры связаны с магнитным потоком 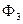 , поэтому по этому уравнению можно построить зависимость
, поэтому по этому уравнению можно построить зависимость  .
.
Составляем таблицу для построения зависимости  :
:
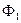
| 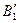
| 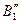
| 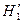
| 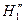
| 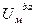
|
 0 0
| 
|
 0 0
| 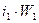
| ||
| 0,2 | … | … | … | … | … |
| … | … | … | … | … | … |
Задаемся 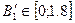 с шагом 0,2 Тл.
с шагом 0,2 Тл.
 по кривой намагничивания определяем
по кривой намагничивания определяем  ,
, 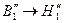 .
.
Подставляя значения в выражение (61), находим 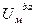 .
.
Составляем таблицу для построения зависимости 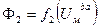 :
:
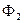
| 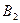
| 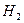
| 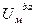
|

| 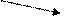
| 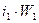
| |
| 0,2 | … | … | … |
| … | … | … | … |
Задаемся 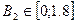 с шагом 0,2 Тл.
с шагом 0,2 Тл.
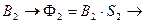 по кривой намагничивания определяем
по кривой намагничивания определяем  .
.
Подставляя значения в выражение (62), находим 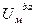 .
.
Составляем таблицу для построения зависимости  :
:
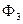
| 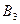
| 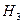
| 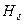
| 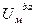
|
| 
 0 0
| |||
| 0,2 | … | … | … | … |
| … | … | … | … | … |
Задаемся 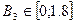 с шагом 0,2 Тл.
с шагом 0,2 Тл.
 по кривой намагничивания определяем
по кривой намагничивания определяем  ,
,  .
.
 Подставляя значения в выражение (60), находим
Подставляя значения в выражение (60), находим 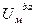 .
.
В соответствии с 1 законом Кирхгофа  строим зависимость
строим зависимость  .
.
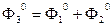
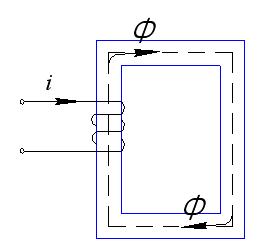 Катушка индуктивности с ферромагнитным сердечником в цепи переменного тока
Катушка индуктивности с ферромагнитным сердечником в цепи переменного тока
1) 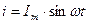
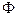 -?
-?
Закон полного тока: 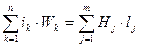 .
.
Для нашей схемы, так как сечение везде одинаковое и материал одинаков, можно записать:
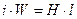
 , т.е. ток пропорционален напряженности.
, т.е. ток пропорционален напряженности.
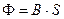 , следовательно, магнитный поток изменяется так же, как индукция.
, следовательно, магнитный поток изменяется так же, как индукция.
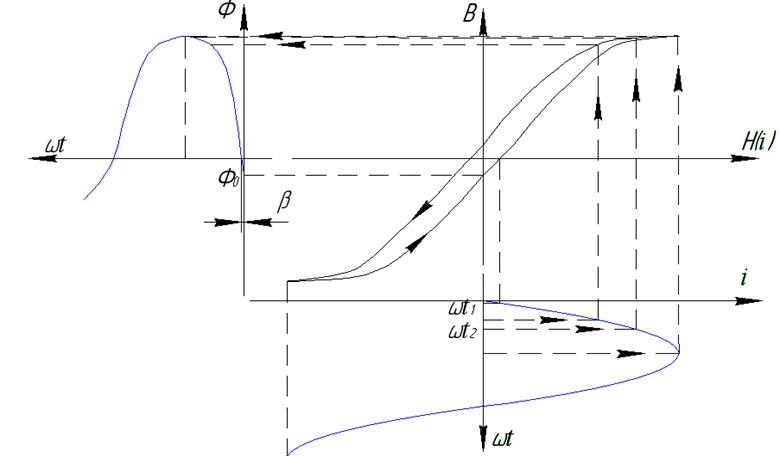
Выводы: 1. При синусоидальном токе магнитный поток не синусоидальный.
2. Первая гармоника магнитного потока отстает от тока на угол 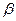 . Величина угла
. Величина угла 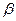 зависит от ширины петли гистерезиса.
зависит от ширины петли гистерезиса.
3. В зоне амплитудных значений магнитный поток имеет форму кривой «приплюснутую».
В соответствии с законом электромагнитной индукции:
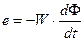
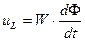
Если мы возьмем первую гармонику магнитного потока:
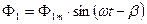
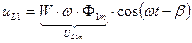
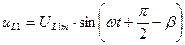
4. Так как магнитный поток не синусоидальный, то падение напряжения на катушке индуктивности тоже будет не синусоидальным.
5. Первая гармоника падения напряжения на катушке индуктивности с ферромагнитным сердечником будет опережать ток на угол  .
.
 2) Пусть
2) Пусть 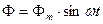 .
.  -?
-?
При  ,
,  ,
,  .
.
Так как 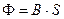 , то
, то  ,
, 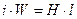 .
.
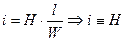
Вывод: 1. При синусоидальном магнитном потоке ток не синусоидальный.
2. Первая гармоника тока опережает магнитный поток на угол 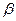 , зависящий от ширины петли гистерезиса.
, зависящий от ширины петли гистерезиса.
3. В зоне амплитудных значений ток имеет резкий выброс.
Общие выводы:
Магнитный поток и падение напряжения на катушку индуктивности связаны следующими соотношениями:
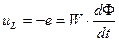
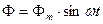
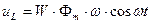
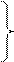
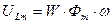
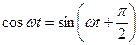
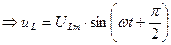
1. При синусоидальном напряжении, приложенном к катушке с ферромагнитным сердечником, ток, протекающий по катушке, будет не синусоидальным.
2. Первая гармоника тока отстает от напряжения на угол  .
.
3. В зоне амплитудных значений напряжений ток резко возрастает.
 Потери в катушке индуктивности с ферромагнитным сердечником
Потери в катушке индуктивности с ферромагнитным сердечником
Различают два вида потерь:
1. 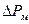 - потери в меди
- потери в меди
2. 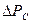 - потери в стали
- потери в стали
 Электрическую схему данной катушки индуктивности можно представить в следующем виде:
Электрическую схему данной катушки индуктивности можно представить в следующем виде:
Потери в меди связаны с активным сопротивлением обмотки  :
:
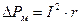
Когда говорят о потерях в стали, говорят о потере энергии в магнитопроводе:
 , где
, где 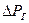 - потери на гистерезис;
- потери на гистерезис;
 - потери на вихревые токи (токи Фуко).
- потери на вихревые токи (токи Фуко).
1)  Потери на гистерезис
Потери на гистерезис 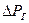
При перемагничивании затрачивается энергия. Так как перемагничивание происходит по разным линиям, то эта энергия зависит от ширины и площади петли гистерезиса.
 - энергия, затрачиваемая на перемагничивание,
- энергия, затрачиваемая на перемагничивание,
где  - коэффициент;
- коэффициент;
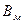 - максимальная магнитная индукция, Тл;
- максимальная магнитная индукция, Тл;
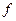 - частота перемагничивания, Гц.
- частота перемагничивания, Гц.
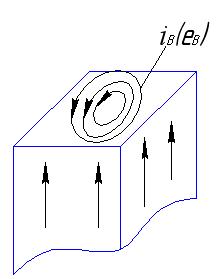
 , где
, где  - объем магнитопровода,
- объем магнитопровода, 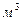 .
.
2) Потери на вихревые токи
Под воздействием пульсирующего магнитного потока в поперечном сечении магнитопровода наводится э.д.с. в соответствии с законом электромагнитной индукции.
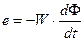
Рассмотрим поперечное сечение. Под воздействием э.д.с. 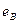 в поперечном сечении как бы по трубкам будут протекать вихревые токи
в поперечном сечении как бы по трубкам будут протекать вихревые токи  . Так как сопротивление этих трубок близко и практически равно 0, то даже при небольших наводимых э.д.с.
. Так как сопротивление этих трубок близко и практически равно 0, то даже при небольших наводимых э.д.с. 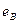 в поперечном сечении будут протекать большие вихревые токи
в поперечном сечении будут протекать большие вихревые токи  , настолько большие, что под их воздействием магнитопровод сильно нагревается и может даже расплавиться. Для уменьшения этого негативного явления в данной схеме магнитопровод изготавливается из пакета листов электротехнической стали.
, настолько большие, что под их воздействием магнитопровод сильно нагревается и может даже расплавиться. Для уменьшения этого негативного явления в данной схеме магнитопровод изготавливается из пакета листов электротехнической стали.
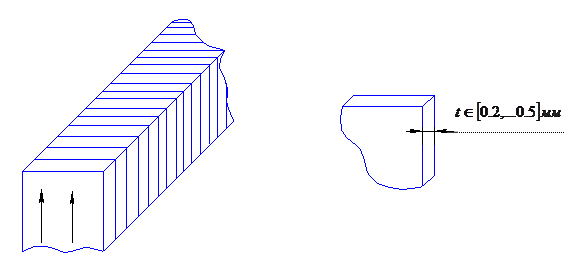
Каждый лист покрыт лаком, и таким образом они изолированы друг от друга. Толщина листов зависит от частоты переменного напряжения. Чем выше частота, тем тоньше лист. Таким образом, сплошные трубки магнитопровода прерываются и остаются только малые контуры внутри каждого листа, по которым будут протекать вихревые токи. Но эти токи значительно меньше, чем в сплошном магнитопроводе. Проявление их действия осуществляется как при легком нагреве магнитопровода, так и в виде гула. Гул объясняется тем, что под воздействием этих токов листы отталкиваются или притягиваются друг к другу. Для того чтобы свести этот фактор к минимуму, магнитопровод стягивается специальными устройствами.
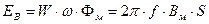
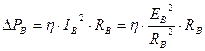
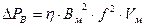
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 2332; Нарушение авторских прав?; Мы поможем в написании вашей работы!