Уравнение неразрывности и уравнение движения

При установившемся режиме работы газопровода (без отборов и подкачек) массовый расход газа, проходящий через любое сечение газопровода, остается постоянным

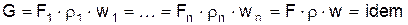, (2.16)

где r – плотность газа;

F – площадь живого сечения газопровода;

w – средняя скорость движения газа;

1¼n – индексы соответственно 1-го и n-го произвольных сечений.

При движении газа происходит значительное снижение давления по длине газопровода вследствие преодоления гидравлического сопротивления. Поскольку газ является сжимаемой средой, плотность газа по длине газопровода уменьшается. Это приводит к возрастанию скорости движения газа. Поэтому для газового потока уравнение баланса удельной энергии можно записать только в дифференциальной форме

. (2.17)

В условиях магистрального газопровода в большинстве случаев можно пренебречь силами инерции 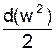и разностью геодезических отметок g×dy.

Тогда уравнение энергии можно переписать в виде

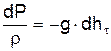. (2.18)

Для решения уравнения (2.18) в случае изотермического установившегося движения газа воспользуемся уравнением состояния

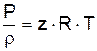, (2.19)

уравнением неразрывности

, (2.20)

уравнением Дарси-Вейсбаха

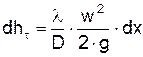, (2.21)

где T – температура газа;

x – продольная координата для произвольного сечения;

D – внутренний диаметр газопровода.

Умножив левую и правую части (2.18) на r² и выразив dh_t с помощью уравнения Дарси-Вейсбаха (2.21), получим

. (2.22)

Выразим значение r в левой части (2.22) из уравнения состояния (2.19), а произведение r×w из уравнения неразрывности (2.20). В результате выражение (2.22) можно представить в виде

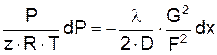
или

. (2.23)

Интегрируя левую часть уравнения (2.23) от P_Н до P_К, а правую от 0 до L, получим

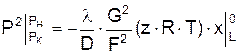. (2.24)

или

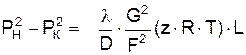, (2.25)

где P_Н, P_К – соответственно давление в начале и конце газопровода;

L – длина газопровода.

Таким образом, выражение (2.25) является решением уравнения движения.

В общем случае коэффициент гидравлического сопротивления l зависит от режима течения (параметра Рейнольдса) и шероховатости внутренней поверхности трубы. Шероховатость трубы для конкретного газопровода – вполне определенная величина. Значение параметра Рейнольдса определяется по формуле

, (2.26)

где Q, G – соответственно объемная и массовая производительность газопровода;

n, m – соответственно кинематическая и динамическая вязкость газа.

Так как динамическая вязкость m зависит от температуры и практически не зависит от давления, то при установившемся движении газа величина параметра Re, а следовательно и значение коэффициента гидравлического сопротивления l по длине газопровода остаются практически неизменными. Например, для газопровода диаметром D = 1,39 м при перекачке газа с относительной плотностью по воздуху D=0,7 значение коэффициента гидравлического сопротивления изменяется в пределах 1% (рис. 2.2).

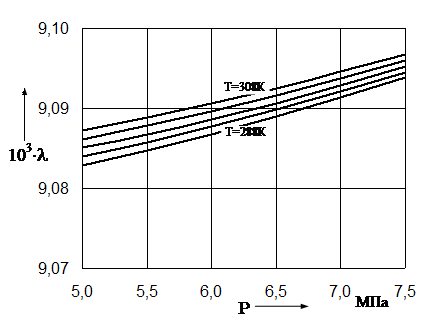Рис. 2.2. Зависимость коэффициента гидравлического сопротивления газопровода от давления и температуры

Если известны давления в начале и конце участка газопровода, уравнение (2.25) можно решить относительно массового расхода газа

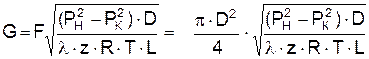. (2.27)

В практических расчетах газопроводов используется понятие коммерческого расхода, то есть объемного расхода газа, приведенного к стандартным условиям (для магистральных газопроводов эти понятия опускаются как само собой разумеющееся). На основании уравнения состояния, а также с учетом D=r/r_В=R_В/R, коммерческий расход составит

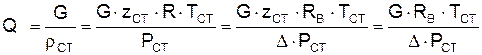, (2.29)

где z_СТ – коэффициент сжимаемости газа при стандартных условиях, z_СТ=1;

D – относительная плотность газа по воздуху;

R_В – газовая постоянная воздуха;

r_СТ – плотность газа при стандартных условиях.

С учетом (2.29) значение коммерческого расхода определяется из выражения

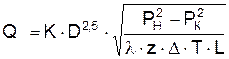, (2.30)

где K – коэффициент, зависящий от размерностей величин, входящих в выражение (2.30), и равный

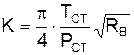. (2.31)

При использовании смешанной системы единиц D(м), T(К), P(МПа), L(км) и Q(млн.м³/сут) значение коэффициента K составляет

K=105,087.

Дата добавления: 2014-01-05