Силы, действующие в жидкости

Капельные и некапельные жидкости

История предмета

250 лет до н.э. Архимед установил принципы гидростатики.

XV в. – Леонардо да Винчи положил начало экспериментальной гидравлике (движение воды в каналах, через отверстия).

XVII в. – Торичелли предложил формулу для определения скорости жидкости, вытекающей из отверстия.

Ньютон высказал основные положения о внутреннем трении в движущихся жидкостях.

XVIII в. – Даниил Бернулли и Леонард Эйлер разработали общие уравнения движения идеальной жидкости (газа).

XIX в. – Шези, Дарси, Базен, Вейсбах начали опытное изучение движения воды в различных частных случаях и получили множество эмпирических формул. Полученные выводы расходились с теоретическими выводами, полученными ранее.

В конце XIX в. – Петров исследовал трение при ламинарном режиме. Рейнольдс изучил переход от ламинарного режима к турбулентному, начал изучать гидравл. сопротивления.

XX в. – Жуковский и Прандтль положили начало изучению турбулентных потоков, неустановившегося движения жидкости.

В связи с развитием авиации, космонавтики, теплоэнергетики, машиностроения, автомобилестроения происходит бурное развитие науки как экспериментальное (лазеры, датчики), так и теоретическое (использование современного математического аппарата, ЭВМ).

В гидравлике, в основном, считается, что жидкость практически не изменяет свой объем под действием внешних сил, т.е. является несжимаемой. К несжимаемым жидкостям относятся все капельные жидкости: вода, нефть, мазут. В отличие от капельных жидкостей, газы (воздух, пропан, бутан и т.д.) легко изменяют объем под действием внешних сил, сжимаются, поэтому их называют сжимаемыми. Любая капельная жидкость может переходить в газообразное состояние при определенной температуре и давлении. Соответственно, газы при понижении температуры и повышении давления могут переходить в жидкое состояние.

На произвольно выделенный объем жидкости действуют два вида сил:

Поверхностные: Р – сила давления Т – сила трения

Массовые: G – сила тяжести I – сила инерции

Массовые силы действуют по всему выделенному объему и пропорциональны его массе 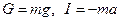. Поверхностные силы действуют по поверхности и пропорциональны площади поверхности.

Рис. 1.1. Напряжение в жидкости

Рассмотрим подробно поверхностные силы. Под влиянием внешних сил, действующих на выделенный объем возникают соответствующие внутренние силы. Проведем внутри объема поверхность S, разделяющую его на две части I и II (см. рис. 1.1). Отбросим часть II и для сохранения равновесия введем силы такие же, как и силы с которыми часть II действовала на часть I. На элементарную площадку Δ s разделяющей поверхности действует сила Δ f. Площадь Δ s может быть стянута в точку М с координатами x, y, z. В этом случае площадь поверхности Δ s, так и сила Δ f стремится к нулю. Отношение силы df к площади поверхности ds стремится к пределу , который называют напряжением.

Силу df, действующую на площадь ds можно разложить на две составляющие: тангенциальную и нормальную. Соответственно, напряжение в жидкости может быть тангенциальным (τ) и нормальным (p). Тангенциальное напряжение, действующее вдоль поверхности ds, называют напряжением трения.

,

(1.1)

где – сила трения площади ds.

Нормальное напряжение, действующее по нормали к поверхности ds, называют напряжением давления или давлением

,

(1.2)

где – сила давления площади ds.

Для площади S можно записать

,

(1.3)

где Т – сила трения площади S.

,

(1.4)

где Р – сила давления площади S. В покоящейся жидкости имеется только нормальное напряжение, тангенциальное напряжение отсутствует.

Сила трения действует вдоль поверхности:

.

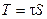(1.5)

Сила давления направлена по нормали к поверхности:

.

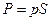(1.6)

Дата добавления: 2014-01-05