Операции наращения и дисконтирования

Бюджетная ответственность

В отличие от налогового законодательства данная глава БК РФ построена по другой системе.

В НК РФ налоговая ответственность – это особый вид ответственности (НК содержит элементы). В БК не закреплено общее понятие бюджетных учреждений, нет понятия вины, нет перечней отягчающих и смягчающих ответственность обстоятельств, нет понятия деликтоспособности.

Конкретные составы БК РФ об отдельных видах правонарушений носят бланкетный (отсылочный) характер.

Когда речь идёт о специфических бюджетных санкциях, следует отметить, что они имеют специфический имущественный характер.

Блокировка расходов – по сути является имущественным ограничением, также как и начисляемые проценты за нецелевое расходование бюджетных средств (ориентиром для начисления процентов выступает ставка рефинансирования Центрального Банка РФ).

В БК РФ установлен бесспорный порядок взыскания каких-либо санкций с нарушителей бюджетного законодательства (в отличие от НК РФ, где налоговые санкции как с физических лиц, так и с организаций могут взыскиваться только в судебном порядке).

БК РФ детально не регулирует процедурную часть, связанную с наложением ответственности.

Логика построения основных алгоритмов достаточно проста и основана на следующей идее. Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы с условием, что через некоторое время будет воз­вращена большая сумма 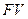. Результативность подобной сдел­ки может быть охарактеризована двояко: либо с помощью абсо­лютного показателя - прироста , либо путем расче­та некоторого относительного показателя. Абсолютные показа­тели чаще всего не подходят для подобной оценки ввиду их не­сопоставимости в пространственно-временном аспекте. Поэто­му пользуются специальным показателем - ставкой. Этот пока­затель рассчитывается отношением приращения исходной сум­мы к базовой величине, в качестве которой можно брать либо , либо 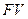. Таким образом, ставка за время рассчитывает­ся по одной из двух формул:

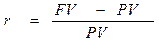(1.1)

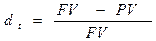(1.2)

В финансовых вычислениях первый показатель имеет назва­ния ''процентная ставка", "ставка процента" (interest rate, rate of interest), "процент", "рост", "норма прибыли" (rate of return), "доходность", а второй - "учетная ставка" (discount rate), "дисконт". Очевидно, что обе ставки взаимосвязаны, т.е. зная один показатель, можно рассчитать другой:

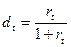или (1.3)

Оба показателя могут выражаться либо в десятичных дробях, либо (как правило, на практике) в процентах. Различие в этих формулах состоит в том, какая величина берется за базу сравне­ния: в формуле (1.1) - исходная сумма, в формуле (1.2) - воз­вращаемая (ожидаемая) сумма. Из определения показателей следует, что и . Случай и 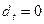не рас­сматривается, так как тогда 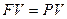(сколько дают в долг, столько и получают назад) и можно считать, что финансовой сделки как таковой просто нет. Случаю же 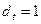соответствует , т.е. не предоставляя никакой суммы в долг, через неко­торое время получаем 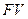, тем самым фактически осуществ­ляя грабеж.

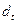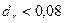Как же соотносятся между собой эти показатели? Очевидно, что всегда , но поскольку также , то . Последнее неравенство позволяет по процент­ной ставке лучше оценить учетную ставку , чем это мож­но сделать, например, используя неравенство . Так, при (т.е. ) из следует , что является существенно более точной оценкой 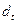, чем .

Степень расхождения между и 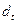зависит от уровня про­центных ставок, имеющих место в конкретный момент времени. Так, если 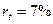, то , т.е. расхождение сравни­тельно невелико; если , то 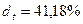, т.е. ставки существенно различаются по величине.

Такой вывод легко обосновать, используя следующие сооб­ражения. В силу того, что , справедливо

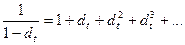
Поэтому

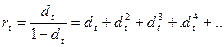
Если величина 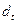достаточно мала, то, пренебрегая в правой части равенств всеми членами, начиная со второго, получим . В частности, если (что равносильно ), то пренебрегаем членами 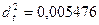, 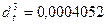и т.д.

В прогнозных расчетах, например, при оценке инвестицион­ных проектов, как правило, имеют дело с процентной ставкой, хотя обычно это не оговаривается. Объяснение этому может быть, например, таким. Во-первых, анализ инвестиционных проектов, основанный на формализованных алгоритмах, может выполняться лишь в относительно стабильной экономике, когда уровни процентных ставок невелики и сравнительно предска­зуемы в том смысле, что их значения не могут измениться в не­сколько раз или на порядок, как это имело место в России в пе­реходный период от централизованно планируемой экономики к рыночной экономике. Если вероятна значительная вариабель­ность процентных ставок, должны применяться другие методы анализа и принятия решений, основанные главным образом на неформализованных критериях. При разумных значениях ставок расхождения между процентной и дисконтной ставками, как мы видели, относительно невелики, поэтому в прогнозных расчетах вполне может быть использована любая из них. Во-вторых, про­гнозные расчеты не требуют какой-то повышенной точности, поскольку результатами таких расчетов являются ориентиры, а не "точные оценки". Поэтому, исходя из логики подобных рас­четов, предполагающих их многовариантность, а также исполь­зование вероятностных оценок и имитационных моделей, из­лишняя точность не требуется.

Кроме введенных показателей часто используют величину, называемую дисконт-фактором (discount-factor):

(1.4)

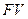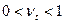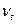Дисконт-фактор показывает, какую часть сумма состав­ляет в сумме . Очевидно, что и между тремя по­казателями справедливо соотношение . Дисконт-фактор может выражаться и в процентах.

Удобной и наглядной характеристикой (особенно при оценке вклада) является индекс роста суммы за время :

(1.5)

Как и прочие введенные показатели, величина выражает­ся либо в десятичных дробях, либо в процентах. Индекс роста показывает, во сколько раз увеличилась первоначальная сумма за время . Зная , можно вычислить и другие показатели. В частности, из (1.5)следует, что .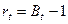

Пример:

Сумма тыс. тенге за полтора года возросла до тыс. тенге Полагая 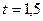года, получим

и 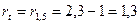(или 130%).

Таким образом, первоначальная сумма за полтора года возросла в 2,3раза, или, что то же самое, увеличилась на 130%.

Индекс роста за данный период показывает, во сколько раз выросла величина капитала по отношению к величине капитала в конце предыдущего периода. Поэтому, если известны индексы роста ,,...,за соответственно периоды времени ,,...,и эти периоды расположены последовательно друг за другом, то индекс роста за время будет ра­вен величине:

(1.6)

Следовательно, если в первый год капитал вырос в 1,2раза, во второй год общий капитал вырос в 1,7раза и в третий год вся сумма увеличилась в 1,3раза, то индекс роста капитала за 3года составит

Итак, в любой простейшей финансовой сделке всегда при­сутствуют три величины, две из которых заданы, а одна являет­ся искомой.

Процесс, в котором заданы исходная сумма и ставка, в фи­нансовых вычислениях называется процессом наращения (accumulation, accretion), искомая величина называется нара­щенной суммой (accumulated value, amount), а ставка — ставкой наращения. Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка, называется процес­сом дисконтирования (discounting), искомая величина называет­ся приведенной суммой, а ставка — ставкой дисконтирования. В первом случае речь идет о движении денежного потока от на­стоящего к будущему, во втором — о движении от будущего к настоящему.

Экономический смысл финансовой операции, задаваемой формулой (1.1),состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Поскольку из формулы (1.1)

(1.7)

то (так как ), т.е. время генерирует деньги.

Естественно, такой же вывод можно сделать, используя фор­мулу (1.2),так как из нее следует, что

(1.8)

и справедливо неравенство .

Разность называется процентом (interest). Это — величина дохода от предоставления в долг денежной суммы . (Заметим, что в математике процентом называют сотую долю некоторого числа, что, естественно, отличается от экономического понятия "процент").

Используя равенство 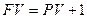, формулу (1.7) можно про­иллюстрировать таким образом:

0

рис. 1. Образование наращенной суммы

Следует отметить, что в качестве ставки наращения может выступать как процентная, так и учетная ставка. Если наращен­ная сумма 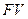находится по формуле (1.7), то ставкой нараще­ния является процентная ставка. С другой стороны, из (1.8) сле­дует, что наращенную сумму можно определять по формуле

,

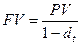поэтому в этом случае ставкой наращения является учетная ставка. (В качестве примера, когда учетная ставка используется для наращения, является учет векселя в банке, рассматриваемый с позиции банка.)

Аналогичные суждения можно высказать и в связи со став­кой дисконтирования. Если приведенная сумма находится по формуле (1.8), то в качестве ставки дисконтирования высту­пает учетная ставка. С другой стороны, из (1.7) следует, что приведенная сумма определяется также и по формуле 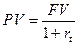, т.е. в качестве ставки дисконтирования выступает процентная ставка. Далее будут подробно рассмотрены процессы наращения и дисконтирования, а из полученных формул или из контекста будет ясно, какая ставка и в каком качестве используется в кон­кретном процессе.

На практике доходность является величиной непостоянной, зависящей главным образом от степени риска, ассоциируемого с тем видом бизнеса, в который сделано инвестирование капита­ла. Связь здесь прямо пропорциональная — чем рисковее биз­нес, тем выше значение доходности. Наименее рисковые вложе­ния в государственные ценные бумаги или в государственный банк, однако доходность операции в этом случае относительно невысока.

Величина 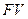, определяемая по формуле (1.7), показывает как бы будущую стоимость "сегодняшней" величины при заданном уровне доходности . Экономический смысл дисконтирования заключается во вре­менном упорядочении денежных потоков различных временных периодов. Одна из интерпретаций коэффициента дисконтирова­ния в формуле (1.8) показывает, какой ежегодный про­цент возврата хочет (или может) иметь инвестор на инвестируе­мый им капитал. В этом случае искомая величина показы­вает как бы текущую, "сегодняшнюю" стоимость будущей ве­личины .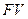

Обозначение является общепринятым сокращением тер­мина present value (текущая, современная стоимость). Анало­гичным образом 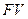представляет собой сокращение для future value (будущая стоимость).

Пример:

Предприятие получило кредит на срок 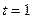год в размере тыс. тенге с условием возврата 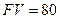тыс. тенге В этом случае процентная ставка , или, что равносильно, ; учетная ставка , или, что равносильно, ; а дисконт-фактор . Если предприятие за взятый кредит через год должно вернуть тыс. тенге, то при учетной ставке 40% по формуле (1.8) можно найти величину кредита тыс. тенге

В общем виде процентная ставка может быть представлена как сумма четырех основных компонент, которые определяют величину :

,

где - норма процента, отражающая компенсацию кредитору за отказ использовать в других целях предоставленную сумму в течение времени (пока не вернут долг);

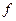- так называемый фактор риска (эффект Фишера), представляющий собой для кредитора компенсацию за неопределенность (риск) непо­лучения процентов или всей суммы вообще при наступлении срока возврата долга;

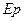- инфляционная добавка, т.е. компенсация за возможное изменение в уровне цен, за уменьшение покупательной способности денег вслед­ствие инфляции;

- компенсация, зависящая от продолжительности срока , на который ссужены деньги, и тем большая, чем длительнее этот срок.

Несколько упрощая для наглядности ситуацию, можно ска­зать, что процентная ставка представляет собой в определенной степени результат взаимодействия хозяйствующих агентов на рынке ссудного капитала.

Пусть DD является кривой спроса на ссудный капитал, от­ражающей зависимость между востребуемым объемом денеж­ных средств и величиной процентной ставки. Естест­венно, с ростом процентной ставки падает спрос на ссудный ка­питал. Аналогичным образом пусть SS является кривой пред­ложения ссудного капитала, показывающей, что с ростом про­центной ставки растет и объем предлагаемых денежных средств. Величина процентной ставки определяется точкой пересече­ния кривых DD и SS, так называемой равновесной точкой, в которой объем спроса равен объему предложения.

Таким образом, как и на рынке продуктов или ресурсов, пересечение кривых спроса на деньги и предложения денег определяет цену равновесия, которая в данном случае является равновесной ставкой. Процентная ставка представляет собой цену, уплачиваемую за использование денег.

3. ПРОЦЕНТЫ "СО 100", "НА 100", "ВО 100"

Приведем ряд задач, часто возникающих в коммерческих расчетах, а также ряд понятий, связанных с этими задачами, ко­торые ранее широко использовались в российской и советской (до начала 50-х годов) практике, да и в настоящее время пред­ставляют определенный интерес.

Пример:

Предприятию перечислили сумму, составляющую р% от Q тенге Найти эту сумму.

Обозначая искомую сумму через R, получим

(1.9)

где (т.е. в отличие от , выраженного в процентах, 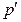выражено десятичной дробью).

Формула (1.9) называется формулой вычисления процентов "со 100", а проценты (R), определяемые по формуле (1.9), на­зываются процентами "со 100" (по отношению к числу Q), т.е. проценты определяются по отношению к самому числу. Про­центная ставка р (или, что эквивалентно, р') по отношению к числу Q называется процентной ставкой "со 100".

Если сумма, перечисленная предприятию, составляет 60% от 150 тыс. тенге, то, вычисляя проценты "со 100" величины 150 тыс. тенге, получим тыс. тенге

Пример:

Фирма реализовала партию товара за S тенге, получив при этом р% прибыли. Найти эту прибыль.

Обозначим себестоимость товара через х, тогда S пред­ставляет собой сумму себестоимости товара (х) и полученной прибыли . Поэтому , откуда . Следовательно, прибыль равна величине

. (1.10)

Формула (1.10) называется формулой вычисления процентов" на 100", а проценты , определяемые по формуле (1.10), называются процентами "на 100" (по отношению к числу S). В этом случае процентная ставка р (или, что эквивалентно, р') по отношению к числу S называется процентной ставкой "на 100".

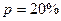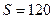Если и тыс. тенге, то тыс. тенге

Очевидно, в частности, себестоимость товара определяется из соотношения тыс. тенге

Проценты "на 100" находят в задачах следующего типа: даны ставка процента и сумма двух слагаемых, одно из которых пред­ставляет собой проценты "со 100" другого; требуется найти од­но из слагаемых. Так, в предыдущем примере данная величина S была равна сумме себестоимости товара и процентов "со 100" (прибыли).

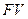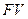Запишем (1.7) в виде , и выразим второе слагаемое (проценты ), используя . Выполняя преобразо­вания, полностью аналогичные тем, которые совершались при решении предыдущего примера, получим . Таким образом, величина дохода (проценты) от предоставления в долг не­которой денежной суммы является процентами "на 100" по от­ношению к и процентами "со 100" по отношению к согласно ставке .

Пример:

Фирма реализовала партию товара за тенге, получив при этом % убытка. Найти этот убыток.

Обозначим себестоимость товара через х, тогда пред­ставляет собой разность между себестоимостью товара (х) и полученного убытка . Поэтому , откуда . Следовательно, убыток равен величине

(1.11)

Формула (1.11) называется формулой вычисления процентов "во 100", а проценты , определяемые по формуле (1.11), называются процентами "во 100" (по отношению к числу К). В этом случае процентная ставка р (или р') по отношению к чис­лу К называется процентной ставкой "во 100".

Если 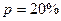и тыс. тенге, то тыс. тенге

Очевидно, в частности, себестоимость товара определяется из соотношения 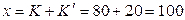тыс. тенге

Проценты "во 100" находят в задачах следующего типа: даны ставка процента и разность двух слагаемых, одно из которых (вычитаемое) представляет собой проценты "со 100" другого; требуется найти одно из слагаемых. В последнем примере дан­ная величина К была равна разности себестоимости и процен­тов "со 100" (убытка).

Запишем (1.8) в виде 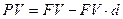и выразим второе слагаемое (проценты ), используя . Таким образом, величина дохода (проценты) от предоставления в долг не­которой денежной суммы является процентами "во 100" по отношению к и процентами "со 100" по отношению к 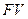согласно ставке .

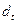Из самих определений ясно, что проценты "со 100" вычис­ляют в так называемых прямых задачах, а проценты "на 100" или "во 100" — в обратных задачах.

Любопытно отметить, что в начале XX в. при помощи формул (1.10) и (1.11) (в отсутствие вычислительных машин и все­возможных калькуляторов) получали правила для составления дробей, упрощающих вычисления процентов.

Если , т.е. , то вычисление процентов "на 100" и "во 100" в определенном смысле сводится к вычислению про­центов "со 100".

Действительно, поскольку в этом случае

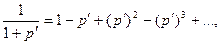
то из формулы (1.10) вычисления процентов "на 100" следует

Рассматривая правую часть равенства, делаем вывод, что - это проценты "со 100" величины ; 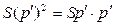- проценты "со 100" полученной величины ; 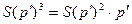- проценты "со 100" величины 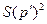и т.д. Аналогичный вывод можно сделать, пользуясь соотношением

и преобразуя формулу (1.11) вычисления процентов "во 100"

В заключение сделаем еще одно замечание в связи с различ­ными видами определенных выше процентов. Очевидно, для любого 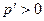справедливо , а если к тому же , то справедливо двойное неравенство 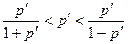. Таким образом, при 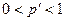, т.е. при , по отношению к одному числу проценты «на 100» меньше процентов «со 100», которые, в свою очередь, меньше процентов «во 100».

Дата добавления: 2014-01-05