Коэфф. (индекс) множественной корреляции

Коэфф. (индекс) множественной корреляции

Корень из R² = R = корень из (SS_R / SS_T)= корень из (1 - SS_E / SS_T);

R = [0; 1] – чем ближе к 1, тем теснее связь (а в парной = [-1; 1]).

Свойства R:

- R - стандартизованный коэффициент регрессии;

- если связи между х и у нет, то R = 0; НО если R = 0, то нет только линейной связи;

- R_ху = R_ух.

Шкала значения коэфф. корреляции:

1. До 0,3 связь слабая 2. 0,3-0,5 связь умеренная

3. 0,5-0,7 связь заметная 4. 0,7-0,9 связь высокая

5. 0,9-1,0 связь весьма высокая, близкая к функциональной.

Скорректированный (нормированный) коэфф. детерминации R²_скорр:

По R²можно сравнивать модели, НО необходимо пересчитать его на число степеней свободы, т.к. модели м. иметь разный набор факторов и разные числовые наблюдения.

R²_скорр = 1 – (SS_E : (n-m-1) / SS_T: (n-1)) = 1 – (1- R²) * ((n-1) / (n-m-1))

R²_скорр всегда больше, чем R²_факт.

22. Показатели частной корреляции

Корень из R² = R = корень из (SS_R / SS_T)= корень из (1 - SS_E / SS_T);

R = [0; 1] – чем ближе к 1, тем теснее связь (а в парной = [-1; 1]).

Свойства R:

- R - стандартизованный коэффициент регрессии;

- если связи между х и у нет, то R = 0; НО если R = 0, то нет только линейной связи;

- R_ху = R_ух.

Шкала значения коэфф. корреляции:

1. До 0,3 связь слабая 2. 0,3-0,5 связь умеренная

3. 0,5-0,7 связь заметная 4. 0,7-0,9 связь высокая

5. 0,9-1,0 связь весьма высокая, близкая к функциональной.

Скорректированный (нормированный) коэфф. детерминации R²_скорр:

По R²можно сравнивать модели, НО необходимо пересчитать его на число степеней свободы, т.к. модели м. иметь разный набор факторов и разные числовые наблюдения.

R²_скорр = 1 – (SS_E: (n-m-1) / SS_T: (n-1)) = 1 – (1- R²) * ((n-1) / (n-m-1))

R²_скорр всегда больше, чем R²_факт.

Показатели частной корреляции о снованы на соотношении сокращения остаточной вариации за счет дополнительно включенного в модель фактора к остаточной вариации до включения в модель соответствующего фактора.

Частные коэфф. корреляции (рекуррентные формулы - выражающие каждый член последовательности через предыдущих членов):

r_yx2.x1 = корень из ((SS_{E yx1} – SS_{E yx1x2}) / SS_{E yx1}) = к. из ((1 – SS_{E yx1x2}) / SS_{E yx1}), х₂ зафиксирован;

r_yx1.x2 = корень из ((SS_{E yx2} – SS_{E yx1x2}) / SS_{E yx2}) = к. из ((1 – SS_{E yx1x2}) / SS_{E yx2}), х₁ зафиксирован.

!!! Матрица частных коэфф. корреляции м.б. использована для отбора факторов в модель.

23. Оценка значимости уравнения множественной регрессии и его параметров

Значение коэфф. детерминации R² может отражать истинную зависимость, а может – стечение обстоятельств, т.к. при построении уравнения используются выборочные данные. Поэтому необходимо определить, насколько выборочные показатели (оценки) достоверны, значимы. Для этого используют вероятностные оценки стат. гипотез.

Статистическая гипотеза (Н) - предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки.

Этапы проверки статистических гипотез:

1. формулируется задача исследования в виде стат. гипотезы;

2. выбирается статистическая характеристика гипотезы;

3. выдвигаются испытуемая и альтернативная Н₀ и Н₁;

4. определяется ОДЗ, критическая область и критическое значение статистического критерия;

5. вычисляется фактическое значение статистического критерия;

6. испытуемая Н₁ проверяется на основе сравнения значений фактического и критического критерия, и в зависимости от результатов проверки Н₁ либо отклоняется, либо принимается.

Критическая область – область, попадание значения статистического критерия в которую приводит к отклонению Н₀. Вероятность попадания значения критерия в эту область равна уровню значимости (1 минус доверительная вероятность).

ОДЗ - область, попадание значения статистического критерия в которую приводит к принятию Н₀.

I. Статистическая оценка достоверности регрессионной модели:

А. 1. выдвигается H₀: r² в генеральной совокупности = 0;

2. выдвигается H₁: r² в генеральной совокупности не = 0;

3. определяется ОДЗ или уровень значимости;

4. рассчитывается критерий Фишера F (n – число единиц совокупности, m – число факторов):

F = MS_R / MS_E = (Σ(y _{с крыш} – y_ср)² / m) / (Σ(y– y _{с крыш})² / (n-m-1))

F = R²/(1-R²) * (n-m-1)/m = R²/ (1-R²) * (n-2);

5. определяется табличное значение критерия Фишера F_табл;

6. фактическое значение сравнивается с табличным.

а. Если F>Fтабл., то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается статистическая значимость и надежность.

б. Если F<Fтабл., то гипотеза о случ… не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

Вывод: с вероятностью α м. утверждать, что коэфф. детерминацииR² в генеральной совокупности не значим; модель недостоверна.

Число степеней свободы (df) - число свободно варьируемых переменных.

df_T = df_R + df_E; n-1 = m + (n – m – 1).

При расчете фактической суммы квадратных отклонений ((у – у_{с крыш}) ² = SS_R) используются теоретические значения результативного признака (у_{с крыш}), определенного по линии регрессии (у_{с крыш} = a + bx). Т.к. объясненная (факторная) сумма квадратов зависит только от n констант, то данная модель имеет n степеней свободы.

Если разделить сумму квадратов на число степеней свободы, можно получить дисперсии на 1-у степень свободы (MS):

MS_R = SS_R/df_R = Σ(y _{с крыш} – y_ср)² / m

MS_Е = SS_Е/df_Е = Σ(y– y _{с крыш})² / (n-m-1)

Все показатели м. оформить в виде таблицы дисперсионного анализа ANOVA.

Источник вариации:	df	SS	MS	F
- регрессия	m	SSR	MSR	F
- остаток	n-m-1	SSE	MSE	–
- итого	n-1	SST	–	–

df – кол-во степеней свободы; MS = SS/df – дисперсия на 1 степень свободы; SS - сумма квадратов отклонений (общ., факт., остат.); F = MS_R/MS_E – критерий Фишера.

Б. Есть частные F-критерии, с помощью которых м. оценить дополнительное включение фактора в модель. Необходимость такой оценки связана с тем, что не каждый фактор в модели существенно увеличивает фактическую вариацию – поэтому нужно ли включать этот фактор в модель?

Важно, что из-за различной связи между факторов, значимость одного и того же доп. фактора различна в зависимости от порядка его включения в модель.

Частные F-критерии строятся на сравнении прироста факторов на 1 степень свободы за счет доп. включения в модель фактора к остаточной вариации до модели.

F_x1 = ((R²_yx1x2 – r²_yx2) / (1-R² _yx1x2)) * (n-m-1) = 0,96

F_x2 = ((R²_yx1x2 – r²_yx1) / (1-R² _yx1x2)) * (n-m-1) = 1,9

F_табл = 10.

Вывод: С вероятностью α м. утверждать, что включение фактора х₁ после х₂ не целесообразно, и включение х₂ после х₁ нецелесообразно – нельзя построить двухфакторную модель.

Все показатели м. оформить в виде частной таблицы дисперсионного анализа ANOVA.

Источник вариации:	df	SS	MS	F
- регрессия	2	SSR	MSR	F
- в т.ч. с ф. х2	1	SSRх2	MSRх2	F х2
- регрессия, обусл. вкл. в модель ф. x1 после x2	1	SSRх1	MSRх1	F х1
- остаток	3	SSE	MSE	–
- итого	5	–	–	–

df – кол-во степеней свободы; MS = SS/df – дисперсия на 1 степень свободы; SS_x2 = SS_T * r_2yx2 - сумма квадратов отклонений (общ., факт., остат.); F = MS_R/MS_E – критерий Фишера. F = t².

II. Оценка значимости коэффициентов регрессии:

1. Выдвигается Н₀: коэффициент регрессии b в генеральной совокупности равен 0;

2. Выдвигается Н₁: коэффициент регрессии b в генеральной совокупности не равен 0;

3. Определяется уровень значимости α;

4. Определяется критическое значение критерия Стьюдента (S_eb – станд. ошибка b; b – коэфф. регрессии,абс. показатель силы связи(в лин. ур-ии), мера зависимости у от х):

t = b/S_eb

S_eb1 = δ_у / δ_х1 * корень из ((1 - R²_yx1x2) / (1- r²_x1x2* (n-m-1))

S_eb2 = δ_у / δ_х2 * корень из ((1 - R²_yx1x2) / (1- r²_x1x2* (n-m-1))

а. t > t_табл., то Н₀ отклоняется, то есть параметр b не случайно отличается от нуля, сформировался под влиянием систематически действующего фактора.

б. t < t_табл., то Н₀ не отклоняется, и признается случайная природа формирования b.

Можно проверить достоверность а (свободный член уравнения регрессии; экономически не интерпретируется):

S_eа = корень из (MS_E / Σ(x-x_ср)²) = корень из (Σ(у-у _{с крыш})²/(n-2)) * Σx²/n* Σ(х- x_ср)²

III. Оценка качества (достоверности) модели

Ошибка аппроксимации (А) – ошибка или остаток.

Можно рассчитать А по каждому наблюдению в относительном виде:

А = (Σ |(у-у _{с крыш}) / у| * 100%) / n

Расчет м. оформить в таблице:

№	y	x	у с крыш	у-у с крыш	|(у-у с крыш) / у| * 100%
	10,57		21,48	-10,91	103,22
	17,50		22,29	-4,79	27,37
…	…	…	…	…	…
Итого:	-	-	-	-	197,15

Если n = 8, то А = 197,15 / 8 = 24,64 %

Если А<10% - норма.

24. Частные критерии Фишера в оценке результатов множественной регрессии

Есть частные F-критерии, с помощью которых м. оценить дополнительное включение фактора в модель. Необходимость такой оценки связана с тем, что не каждый фактор в модели существенно увеличивает фактическую вариацию – поэтому нужно ли включать этот фактор в модель?

Важно, что из-за различной связи между факторов, значимость одного и того же доп. фактора различна в зависимости от порядка его включения в модель.

Частные F-критерии строятся на сравнении прироста факторов на 1 степень свободы за счет доп. включения в модель фактора к остаточной вариации до модели.

F_x1 = ((R²_yx1x2 – r²_yx2) / (1-R² _yx1x2)) * (n-m-1) = 0,96

F_x2 = ((R²_yx1x2 – r²_yx1) / (1-R² _yx1x2)) * (n-m-1) = 1,9

F_табл = 10.

Вывод: С вероятностью α м. утверждать, что включение фактора х₁ после х₂ не целесообразно, и включение х₂ после х₁ нецелесообразно – нельзя построить двухфакторную модель.

Все показатели м. оформить в виде частной таблицы дисперсионного анализа ANOVA.

Источник вариации:	df	SS	MS	F
- регрессия	2	SSR	MSR	F
- в т.ч. с ф. х2	1	SSRх2	MSRх2	F х2
- регрессия, обусл. вкл. в модель ф. x1 после x2	1	SSRх1	MSRх1	F х1
- остаток	3	SSE	MSE	–
- итого	5	–	–	–

df – кол-во степеней свободы; MS = SS/df – дисперсия на 1 степень свободы; SS_x2 = SS_T * r_2yx2 - сумма квадратов отклонений (общ., факт., остат.); F = MS_R/MS_E – критерий Фишера. F = t².

а. Если F>Fтабл., то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается статистическая значимость и надежность.

б. Если F<Fтабл., то гипотеза о случ… не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

Вывод: с вероятностью α м. утверждать, что коэфф. детерминацииR² в генеральной совокупности не значим; модель недостоверна.

25. Использование фиктивных переменных в моделях множественной регрессии

Фиктивная (структурная) переменная – переменная, принимающая значение 1 или 0.

Используется при решении следующих задач:

1. при моделировании качественных признаков;

2. для учета структурной неоднородности, к которой приводят качественные признаки;

3. для оценки сезонных колебаний.

Фиктивные (структурны) переменные – это сконструированные искусственно переменные, например, пронумерованные атрибутивные признаки (пол, образование, регион).

Рассмотрим пример:

Дано: Z=0, если камина в доме нет; Z=1, если камин в доме есть.

- Рассчитаем показатели тесноты (R²) и силы (b, Э) связи.

- Оценим значимость (достоверность) параметров модели (t) и самой модели (F, F_частн).

- Общий вид уравнения: Y = 50 + 16X + 3Z.

Вывод: Для домов, не имеющих камина: Y = 50 + 16X (поскольку Z =0); для домов, имеющих камин: Y = 5 + 3 + 16X = 53 + 16Х (поскольку Z =1).

Вывод:

1. Увеличение жилой площади на 1000 кв.футов приводит к увеличению предсказанной средней оценочной стоимости на 16 тыс.долл. (это b) при условии, что фиктивная переменная (наличие камина) имеет постоянное значение.

2. Если жилая площадь постоянна, наличие камина увеличивает среднюю оценочную стоимость дома на 3 тыс.долл. (это коэфф. перед Z = c).

!!! Фиктивные переменные м. вводится и в нелинейные модели. При этом они вводятся линейно.

Рассмотрим пример:

ln y = ln a + b₁ln x₁ + b₂z; ln y = 4 +0,3 ln x + 0,05z

y_{c крыш} = e⁴ x^0,3 e^0,05z e⁴ = 65 e^0,05z = 1,05

y = a + b₁z₁ +b₂z₂

Параметр a - среднее значение результативного признака при z₁, z₂ = 0.

Параметр b1 и b2 характеризует разность средних уравнений результативного признака для группы 1 и базовой группы 0.

Параметр b2 характеризует разность средних уравнений результативного признака для группы 2 и базовой группы 0.

Вывод:

1. 0,3 – коэфф. Э: при увеличении площади на 1 %, стоимость увеличивается на 0,3 %.

2. e^0,05z - оценка стоимости домов с камином в 1,05 раз дороже (на 5 %), чем без него.

26. Предпосылки метода наименьших квадратов

МНК применяется при оценке уравнения регрессии. Делаются предпосылки относительно случайной составляющей ε (ненаблюдаемой величиной): y = a + b₁х₁ +b₂х₂ + … + ε.

Основные предпосылки МНК:

1. случайный характер остатков (если на поле корреляции нет направленности в расположении точек ε);

2. нулевая средняя остатков, не зависящая от фактора x: Σ(у - у_{х с крыш}) = 0 или нелин. модель - Σ(ln у - ln у_{х с крыш}) = 0 и также на поле корреляции …;

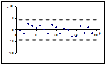3. гомоскедастичность (дисперсия каждого

отклонения одинакова для всех значений x);

4. отсутствие автокорреляции остатков

(распределение остатков независимо друг от друга);

5. остатки должны подчиняться нормальному распределению.

Если все 5 предпосылок выполнены, то оценки, полученные МНК и методом максимального правдоподобия, совпадают. Если не все – нужно скорректировать модель.
27. Гетероскедастичность - понятие, проявление и меры устранения

Проблемы, возникающие при построении регрессионных моделей:

1. Гетероскедастичность.

2. Мультиколлинеарность.

Гетероскедастичность (неоднородность) — означает ситуацию, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации МНК (иначе возможны ошибочные выводы).

Г. проявляется, если совокупность неоднородна (изучаются разносторонние области).

Симптомы Г.:

1. низкий коэффициент детерминации r²;

2. это м. привести к смещенности оценки.

Меры по устранению гетероскедастичности:

1. Увеличение числа наблюдений.

2. Изменение функциональной формы модели.

3. Разделение исходной совокупности на качественно-однородные группы и проведение анализа в каждой группе.

4. Использование фиктивных переменных, учитывающих неоднородность.

5. Исключение из совокупности единиц, дающих неоднородность.

Зависимость остатков от выровненного значения результата:

а. дисперсия остатков увеличивается с

увеличением выровненного значения

результата (один из случаев Г.).

б. нет зависимости (гомоскедастичность). а) б)

Тесты, используемые для выявления Г.:

1. Гольдфельда-Квандта

2. Парка

3. Глейзера

4. Уайта

5. Ранговой корреляции Спирмена

28. Оценка гетероскедастичности с помощью метода Гольдфельда и Квандта

Гетероскедастичность (неоднородность) — проблема, возникающая при построении регрессионных моделей; означает ситуацию, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации МНК (иначе возможны ошибочные выводы).

Г. проявляется, если совокупность неоднородна (изучаются разносторонние области).

Этот метод используется при малом объеме выборки. Рассмотрели однофакторную модель, для кот. дисперсия остатков возрастает пропорционально квадрату фактора. Чтобы оценить нарушение Г., предложили параметрический тест.

1. Все наблюдения упорядочивают по мере возрастания какого-либо фактора, который, как предполагается, оказывает влияние на возрастание дисперсии остатков.

2. Упорядоченную совокупность делят на три группы, причем первая и последняя должны быть равного объема с числом единиц, больших, чем число параметров модели регрессии. Число отобранных единиц обозначим k

Дата добавления: 2014-01-05