
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частный критерий Фишера
|
|
|
|
Оценка существенности параметров линейных уравнений множественной регрессии
Существенные и несущественные параметры
Суть проверки существенности параметров регрессии сводится к тому, что принимается либо отвергается нулевая гипотеза о равенстве нулю соответствующего параметра.
Если эта гипотеза принимается, то параметр считают несущественным. Это означает, что вероятность того, что отличие параметра от нуля является случайным, велика (больше заданного уровня значимости). При равенстве параметра нулю можно сделать вывод, что соответствующий фактор не следовало включать в модель.
Если нулевая гипотеза отвергается, то отличие параметра от нуля можно считать существенным, следовательно, получен существенный параметр.
Показатели существенности параметров
Для оценки существенности коэффициентов множественной регрессии можно использовать критерии Стьюдента и Фишера, а также рассчитывают доверительные интервалы.
Рассмотрим частный критерий Фишера более подробно. Он рассчитывается для отдельных факторов и представляет собой сравнение прироста объясненной дисперсии под влиянием включения в модель нового фактора к остаточной дисперсии модели, включающей все факторы:
|

где xj – тот фактор, для которого рассчитывается частный критерий Фишера;
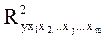 - коэффициент детерминации для модели, включающей все факторы;
- коэффициент детерминации для модели, включающей все факторы;
 - коэффициент детерминации для модели, включающей все факторы, кроме xj.
- коэффициент детерминации для модели, включающей все факторы, кроме xj.
Поскольку увеличение объясненной дисперсии в числителе связано с включением одного дополнительного фактора, число степеней свободы для нее будет равно единице. Отсюда число степеней свободы распределения Фишера k1 = 1 и k2 = n – m – 1.
Если фактическое значение критерия Фишера будет больше табличного при заданном уровне значимости, то соответствующий параметр множественной регрессии aj можно считать значимым, и включение в модель фактора xj является оправданным с точки зрения увеличения объясненной вариации результата.
При получении фактического значения, меньшего или равного табличному, придется сделать вывод о несущественности, статистической незначимости соответствующего параметра.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 3537; Нарушение авторских прав?; Мы поможем в написании вашей работы!