Типы данных. Классификация эконометрии

Классификация эконометрии.

Отметим, что существует множество классификаций эконометрических моделей в зависимости от выбранных признаков классификации. Ниже приводится достаточно простая и удобная классификация.

1.6.1. По структуре уравнений регрессии

1). Аддитивные (полиноминальные) уравнения регрессии представляются в виде суммы базисных функций с соответствующими коэффициентами:

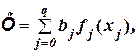(1.10)

где, {¦ _j (х _j)} - совокупность базисных (координаторных) функций.

Пример:

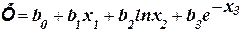
2). Мультипликативная форма в виде произведения базисных функций

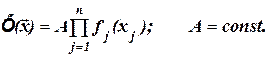(1.11)

Примером такой модели является модель Брандона:

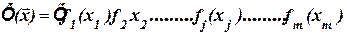
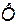– математическое ожидание (среднее).

1.6.2. По способу учета динамики:

1. Динамические многофакторные.

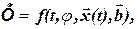(1.12)

где, t – время.

2. Квазистатические.

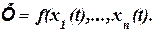(1.13)

3. Динамические с лаговыми переменными.

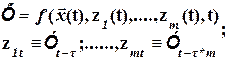(1.14)

здесь t – временной лаг (запаздывание).

4. Статические.

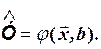(1.15)

Замечание: Введение в модель лаговых переменных – весьма эффективный прием, который позволяет наряду с основным («быстрым») временем t учесть динамические процессы с большей постоянной времени, т.е. «медленное» время а, значит, предысторию процесса, что важно в эконометрических объектах [, ].

1.6.3. По виду связи между .

Можно выделить модели:

1. Регрессионные (аддитивные и мультипликативные).

2. Системы одновременных уравнений – когда модель состоит не из одного уравнения, а нескольких, т.е. в правой части этих уравнений стоят компоненты векторов 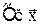, т.е. четко не разделены причины и следствия.

3.Рекурсивные – частичный случай системы одновременных уравнений. В рекурсивных моделях система одновременных уравнений «расщепляются» по рекуррентному алгоритму.

1.6.4. По алгоритму оценки параметров модели.

1. Неадаптивные (метод наименьших квадратов, поисковые методы, алгоритмы нечеткой регрессии, и др.)[ ].

2. Адаптивные (обучаемые, включая нейросенсорный метод).

Замечание: На практике классификационные признаки могут «переплетаться», т.е. использоваться комбинированные (гибридные) модели, например нейро-нечеткие [ ], нечеткие регрессионные и др.

1.7.1. Данные пространственного типа

База данных состоит из кортежей:

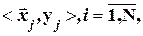
которые образуют матрицу. Каждая строка матрицы – это кортеж (или вектор строка таблицы исходных данных).

Здесь основное требование – независимость наблюдений {y _j } между собой, т.е. {y_j} – случайные (измеренные независимо) величины в данном фиксированном временном срезе, где t=const, это влечет за собой условие отсутствие коррелированности возмущений.

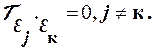(1.16)

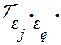– коэффициент корреляции.

Как определить, является ли база данных серией независимых наблюдений? Однозначного ответа нет, т.е. это условие реально труднопроверяемо. Считается, что {Y_i} не должны быть связаны причинно [ ].

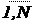Совокупность кортежей для всех наблюдений i= (таблица) в фиксированном временном срезе есть входные данные пространственного типа.

1.7.2. Временной (динамический) ряд

Здесь наблюдения упорядочены во времени: {У_t}, t=t₁,t₂,….t_i,…t_n; где t_i>t_i-1

а). Чаще всего Dt = t_i - t_i-1 = const. Тогда в записи указывается только номер временного интервала {У_t}- временной ряд.

б). Временной ряд может быть многомерным: {У_t, х_1t,…x_nt} (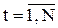), т.е. другими словами:

если наблюдаются одновременно несколько независимых случайных величин в каждом временном срезе, t=t₀, то имеем многомерный временной ряд:

Данные типа многомерного временного ряда

Таблица 1.1.

ti	t1	t2	….	tn
yi	y1	y2	….	yn
хi	х1	х2	….	хn
zi	z1	z2	….	zn

Данные типа многомерных временных рядов имеются часто в многофакторных прогнозных моделях.

Дата добавления: 2014-01-05