Описание поверхностей

Параметрическое описание поверхностей.

Параметры – независимые величины, предназначенные для выделения элемента либо подмножества из множества. В геометрических задачах параметрами могут быть величины, выделяющие единственную фигуру из множества подобных фигур (задание в качестве параметров длины стороны треугольника и величины двух прилегающих к ней углов приводит к выделению единственного треугольника).

При выделении параметров важно учитывать области их существования (числа, выражающие длины сторон треугольника, могут быть только положительными и отличными от нуля, сумма любых двух из этих чисел должна быть больше третьего числа).

Поверхности, заданные в форме X = X (u, t), Y = Y (u, t), Z = Z (u, t), где u, t – параметры, изменяющиеся в заданных пределах, относятся к классу параметрических. Для одной фиксированной пары значений u, t можно вычислить только положение одной точки поверхности. Для полного представления о всей поверхности необходимо с определенным шагом перебрать множество пар u, t из диапазона их изменений, вычисляя для каждой пары значение X, Y, Z в трехмерном пространстве.

Эллипсоид вида

параметрически представляется в форме

,

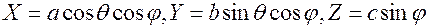где q – долгота, j – широта. q = [0; 2p]; j = [-p/2; p/2]

Особенно важными в практическом применении являются бикубические поверхности, с помощью которых можно описать гладкую поверхность произвольной формы. функция, составленная из нескольких смежных бикубических участков, будет обладать непрерывностью и гладкостью в местах стыка благодаря координатному совпадению смежных угловых точек и совпадению первых производных. Участок такой поверхности X = X (s, t), Y = Y (s, t), Z = Z (s, t) может быть представлен параметрически, например, уравнение для X = X (s, t):

,

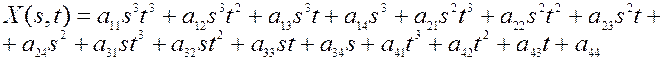где s, t – параметры, изменяющиеся в некотором фиксированном диапазоне; а₁₁,…,а₄₄ – постоянные коэффициенты в пределах данной поверхности, которые могут быть объединены в матрицу С_х размера 4х4.

Аналогичные выражения существуют для Y (s, t), Z (s, t), соответственно матрицы коэффициентов будут С_у, С_z.

Основной задачей конструирования криволинейной поверхности из бикубических участков является задание коэффициентов бикубического многочлена С_х, С_у, С_z внутри каждого участка через координаты общих угловых точек.

Обычно бикубические участки – это гладкие изогнутые четырехугольники, представление о которых могут дать листы металла, бумаги и др. материалов, обладающих упругостью.

Недостатки этой формы задания: трудоемкость описания и большие вычислительные затраты ввиду необходимости применения численных, а не аналитических методов математических решений.

Основное преимущество параметрического описания – возможность передачи геометрической формы очень сложных поверхностей, которые др. методами описать очень сложно.

Например, винтообразная улитка может быть описана параметрическим представлением суммы трех векторов: первого, вокруг которого завивается улитка; второго, конец которого очерчивает спираль, а начало скользит по первому; и третьего, начало которого скользит по спирали, а конец вращается вокруг спирали.

Тор, симметричный относительно оси OZ и плоскости XOY:

где а – радиус кольцевого "баллона" тора; R – расстояние от центра тора до оси "баллона"; u = [0, 2p], q = [0, 2p]. Неявное описание вида f (X, Y, Z) = 0 этих поверхностей невозможно.

Другое преимущество параметрического описания заключается в приспособленности к физическим процессам управления резцом в станках с числовым программным управлением. Резец в этом случае должен вытачивать деталь, двигаясь в пространстве по законам, заданным в параметрической модели.

Параметрические поверхности очень легко ограничиваются в пространстве путем задания пределов изменения параметров. Например, наружная поверхность дольки апельсина в виде 1/8 шара радиуса r задается в виде X = r sin u cos q, Y = r sin u sin q, Z = r cos u, q = [0, p/4], u = [-p/2, p/2]. Описание ограничений в неявно заданных поверхностях гораздо более сложно.

Описание поверхности неявными функциями. Заключается в моделировании поверхностей следующей математической формой: f (X, Y, Z) = 0, где X, Y, Z – координаты объектного пространства.

В качестве функции f могут быть функции различных порядков, однако из-за сложности математической обработки обычно ограничиваются первой и второй степенью. Существуют аналитические методы решения уравнений третьей и четвертой степени, однако поверхности, описываемые функциями такой степени, незначительно расширяют возможности геометрической имитации форм, а вычислительные затраты резко возрастают. Поверхности первого порядка вида AX + BY + CZ + D = 0, где A, B, C, D – коэффициенты, представляют собой плоскости.

Из поверхностей первого порядка можно составить описание поверхности объекта типа полигонального поля. Таким полем называют серию смежных многоугольников, не имеющих разрывов между собой. Каждое ребро поля является общим для смежных многоугольников. Таким образом, составная функция, описывающая поверхность, обладает непрерывностью, а производная имеет разрывы в местах стыка участков плоскостей.

Поверхности второго порядка типа

AX² + BY² + CZ² + DXY + EYZ + FZX + GX + HY + JZ + K = 0

в зависимости от значения коэффициентов А – К могут описывать две плоскости, конусы, гиперболоиды, параболоиды и эллипсоиды. Неявная форма задания поверхности хорошо подходит для использования в методе твердотельного моделирования и при трассировании лучей, так как существуют простые приемы определения взаимного положения точки и поверхности такого типа, определения точки пересечения прямой и поверхности.

Поточечное описание поверхностей – представление поверхности множеством отдельных точек, принадлежащих этой поверхности. Теоретически при бесконечном увеличении числа точек такая модель обеспечивает непрерывную форму описания. Точки, используемые для описания, должны располагаться достаточно часто, чтобы можно было передать поверхность без грубых потерь и искажения информации. Основная особенность такого описания – отсутствие информации о поверхности между точками. Например, при задании полигональных поверхностей вершины каждого плоского полигона, а следовательно, и вся модель могут быть описаны точками, но предполагается, что между точками располагаются участки плоскостей.

Поточечное описание поверхностей применяют в тех случаях, когда поверхность очень сложна, не обладает гладкостью, а детальное представление многочисленных геометрических особенностей важно для практики (участки грунта на других планетах, формы малых небесных тел). Исходная информация при данном методе описания представляется в виде матрицы трехмерных координат точек.

Поверхности типа экструзий. Extrusion – выталкивание, выдавливание. Это: металлические профили, выдавленные из расплава, поверхности вращения, вырезанные резцом из заготовки. Большой класс деталей может быть представлен как результат вращения кривой или ломаной линии относительно некоторой оси.

Кривую линию, являющуюся линией вращения фигуры, аппроксимируют ломаной линией. Каждый отдельный участок последней становится образующей отдельного конуса. Описание конуса может быть как неявным, так и параметрическим в зависимости от алгоритма синтеза изображения.

Другими представителями поверхностей-экструзий являются поверхности, образованные путем параллельного переноса кривой линии вдоль некоторой прямой. Кривую аппроксимируют ломаной линией, а всю поверхность фигуры представляют множеством смежных четырехугольников. Две стороны каждого четырехугольника параллельны направляющей прямой, а две остальные параллельны соответствующему отрезку ломаной. Если в качестве направляющей используется кривая линия, то она тоже аппроксимируется ломаной.

Модели объектов и их классификация

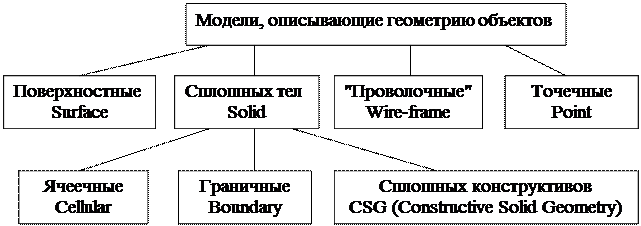
Три основных типа: описание объекта поверхностями, сплошными телами и типа проволочной сетки (каркасом).

Проволочная модель или каркасное моделирование. Поверхность представляется серией пересекающихся линий, принадлежащих поверхности объекта. Каркасная модель полностью описывается в терминах точек и линий. Каркасное моделирование представляет собой моделирование самого низкого уровня и имеет ряд серьезных ограничений, большинство из которых возникает из-за недостатка информации о гранях, заключенных между ребрами, и невозможности выделить внешнюю и внутреннюю области изображения твердотельного объема.

Главный недостаток – неоднозначность распознавания ориентации и видимости граней каркасного изображения. В отличие от твердотельной модели, в каркасной нельзя отличить видимые грани геометрической формы от невидимых (скрытых).

Описание объекта поверхностями. Объект представляется в виде тонких поверхностей, под которыми находится пустое пространство, не заполненное материалом объекта (эллипсоид – пустое внутри яйцо). В рамках этого метода конструируют полигонные поля и бикубические участки. Это модель более высокого уровня, чем каркасная, более гибкая и функциональная. Поверхности описываются различными способами (рассмотрено выше).

Описание сплошными телами. Объекту или отдельному примитиву принадлежат все точки объекта или примитива – как наружные, так и внутренние (эллипсоид – однородно заполненное яйцо). Модель описывается в терминах того трехмерного объема, который занимает определяемое ею тело.

Преимущества:

– полное определение объема и формы;

– обеспечение автоматического удаления невидимых (скрытых) линий;

– автоматизированное построение трехмерных разрезов проектируемого изделия, что особенно важно при анализе сложных сборочных единиц;

– автоматическое получение точных значений массы, площади поверхности, центра тяжести, момента инерции для любой детали или изделия в целом;

– повышение эффективности имитации движения инструмента или рабочих органов изделия;

– наличие разнообразной палитры цветов, получение тоновых эффектов – качественное изображение формы.

Описание сплошными телами

Ячеечные методы. Ограниченный участок пространства, охватывающий весь моделируемый объект, считается разбитым на большое число дискретных кубических ячеек. В простейшем случае размеры ребра куба равны единице измерения длины. Моделирующая система должна просто записать информацию о принадлежности или непринадлежности каждого куба телу объекта. Структура данных представляется трехмерной матрицей, в которой каждый элемент соответствует пространственной ячейке. Преимущество – прост, недостатки – требуется большой объем памяти для записи объекта с высоким разрешением. Для преодоления этого недостатка можно ячейки, которые захватывают границу объекта, разбить на подъячейки меньшего размера.

Представление объекта границами. В памяти машины сохраняют все элементы, которые создают границы объекта. Это: поверхности, края поверхности и указатели пересечений поверхностей. Также необходимо записать топологическую информацию, которая показывает, как элементы связаны друг с другом. Поверхности края и пересечения являются топологической основой конструкции объекта. При моделировании объекта границами структура данных строится одновременно с процессом создания модели. Преимущества: большие возможности геометрического моделирования форм, чем при описании сплошными телами; быстрый и эффективный доступ к геометрической информации, которая требуется для выполнения сечений тел или др. прикладных целей; относительно простое создание геометрических поверхностей свободных форм. Недостатки: больший объем исходных данных, чем при твердотельном моделировании; модель логически менее устойчива, чем твердотельная, т.е. возможно создание противоречивых конструкций; сложности построения вариаций форм.

Моделирование сплошными геометрическими конструктивами (твердотельное моделирование). Сложные объекты представляются составленными из простых объемных примитивов (кубы, цилиндры, конусы, эллипсоиды и др.). Основан на использовании булевых операций. Булевы операции над примитивами позволяют достигать объединения, вычитания и выделения общей части примитивов.

Над примитивами допустимы следующие пространственные операции взаимодействия друг с другом: "+" – объединение, "&" – пересечение, "–" – вычитание.

Объединением или суммой примитивов П₁ и П₂ называется тело, каждая точка которого принадлежит хотя бы одному из объединяющихся примитивов:

(·) А Î (П₁+П₂), если (·) А Î П₁ или (·) А Î П₂.

Пересечением или общей частью примитивов П₁ и П₂ называется тело, каждая точка которого одновременно принадлежит обоим примитивам:

(·) А Î (П₁&П₂), если (·) А Î П₁ и (·) А Î П₂.

Вычитанием примитива П₁ из П₂ называется тело, каждая точка которого принадлежит П₁, но не принадлежит П₂:

(·) А Î (П₁–П₂), если (·) А Î П₁ и (·) А Ï П₂.

Любой пространственный объект, образованный комбинацией примитивов можно описать структурой, вершиной которой является сам объект, корнями – примитивы, а в узлах ветвей определены операции пространственных комбинаций. Операция "– П" (взятие дополнения) означает, что подразумевают объект, занимающий все трехмерное пространство за исключением точек, принадлежащих поверхности и внутренней области примитива П. Результат операции называют отрицанием примитива. П₁ – П₂ = П₁ & (– П₂).

Множество примитивов П₁, П₂, …, все трехмерное пространство I и пространство нулевого объема Е (пустое пространство) образуют булеву алгебру. Некоторые свойства булевой алгебры:

П₁ + Е = П₁, П₁ & Е = Е

П₁ & I = П₁, П₁ + I = I

П₁ + (–П₁) = I, П₁ & (–П₁) = E

–I = E, –E = I и др.

П₁ П₂ П₁+П₂ П₁&П₂ П₁-П₂ П₂-П₁

П₁ П₂ П₃ О

Преимущества: простота, малый объем требуемой памяти, невозможность создания противоречивых конструкций, приспособленность к усложнению модели, относительная простота представления частей и сечений общего объекта. Недостатки: метод построения объекта ограничен рамками булевых операций, невозможность использования параметрически описанных поверхностей, сложности создания и обработки объектов, поверхность которых описана функциями более чем второй степени.

Понятие функции принадлежности

Введенные правила задания примитивов позволяют формальными методами определять взаимное расположение любой точки и конкретного примитива. Зная правила объединения примитивов в объект, можно определить взаимное положение точки и объекта. Взаимное положение характеризуется функцией принадлежности j(X, Y, Z; Ф), где X, Y, Z – координаты точки; Ф – обозначение примитива, объекта или другой фигуры. Функция j = –1, если точка находится вне объекта Ф, j = 0, если точка лежит на поверхности Ф; j = +1, если точка лежит внутри Ф.

Этот факт зависит от взаимного расположения точки и примитивов и правила пространственного комбинирования примитивов.

Правила определения положения точки

по отношению к комбинации пары примитивов А и В

j(А)	j(В)	j(–А)	j(А–В)	j(В–А)	j(А+В)	j(А&В)
–1 –1 –1	–1 –1 –1	–1 –1 –1	–1 –1 –1 –1 –1 –1	–1 –1 –1 –1 –1 –1	–1	–1 –1 –1 –1 –1

Под примитивами А и В понимаются пространственно ограниченные выпуклые трехмерные тела. На основании составленной таблицы формальными методами может быть определено положение точки по отношению к сложному объекту, состоящему из многих примитивов.

Пример. Пусть точка лежит на поверхности С, вне А, внутри В: j(С) = 0; j(А)=–1; j(В)=1. Объект задается описанием О = (А–В)&С. Чисто формально по таблице сначала определяем j(А–В)= –1. Далее также по таблице j(–1; 0) = –1. Этот результат означает, что точка лежит вне объекта.

Технические средства САПР

Пасьянс "Косынка" наносит мировой экономике ущерб примерно 800 трлн. долл. ежегодно, за счет потери рабочего времени.

Дата добавления: 2014-01-05