Лекция № 2. Введение в теорию графов(продолжение)

Определение 23: Отображение 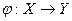называется взаимнооднозначным, если

.

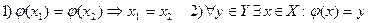Определение 24: Взаимнооднозначное отображение множества вершин графа 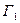на множество вершин графа 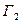и ребер (дуг) 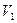на 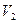, сохраняющее отношение инцидентности, называется изоморфизмом графов 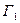и :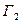

.

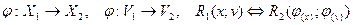Замечание. В простом графе достаточно определить изоморфизм на множестве вершин.

Определение 25. Граф, изоморфный части графа 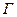, называется подграфом .

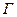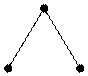
Рис 2. Подграф.

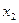
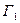
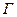
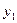
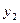
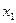
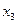
Определение 26. Граф 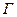называется плоским (планарным), если его можно изоморфно отобразить на граф 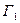, расположенный на плоскости без самопересечений.

Рис 3. Плоский граф.

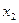
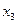
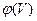
V

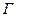
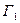
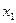
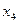
Утверждение 3. Композиция изоморфизмов и обратное изоморфизму отображение сами являются изоморфизмами.

Теорема 2. Следующие величины и свойства являются инвариантами графа 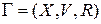, то есть сохраняются при изоморфизмах:

1). 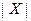- число вершин графа;

2). 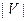- число ребер и дуг графа;

3). - число дуг графа;

4). 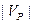- число ребер графа;

5). 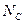- число циклов в графе;

6). 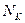- число контуров в графе;

7). - число петель в графе;

8). 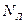- число листьев в графе;

9). 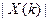- число вершин графа степени ;

10). - число вершин графа полустепени захода ;

11). 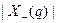- число вершин графа полустепени исхода ;

12). Связность графа;

13). Эйлеровость, гамильтоновость и планарность графа;

Определение 27. Редукцией графа называется «стирание» вершины степени .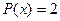

Рис 4. Редукция графов.

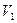
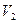
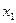
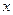
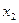
редукция

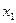
Утверждение 4. Если редуцированный граф не плоский, то и сам граф неплоский.

Утверждение 5. Если подграф не плоский, то и сам граф неплоский.

Теорема 3. Граф не является плоским тогда и только тогда, когда с помощью операций перехода к подграфу и редукции он сводится к одному из двух стандартных неплоских графов .

Рис 5. Стандартные неплоские графы.

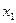
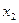
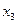
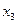
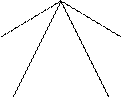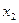
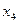
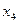
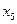
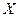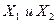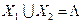Определение 28. Граф называется двудольным, если множество его вершин можно разбить на два таких непересекающихся множества (доли), что и (где 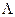- пустое множество), причем – смежные только, если , а 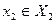или наоборот . Если при этом каждая вершина множества соединена с каждой вершиной множества , то двудольный граф называется полным двудольным графом.

Граф – полный двудольный, а - просто полный.

Определение 29. Граф называется связным, если любые две вершины можно соединить некоторой цепью.

Рис 6. Связные и несвязные графы.

Связный Несвязный.

Определение 30. Связная компонента графа - это максимальный связный подграф.

Рис 7.

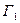
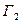
– связные компоненты.

Теорема 4. Каждая вершина графа содержится в некоторой связной компоненте.

Доказательство. Возьмем вершину графа и все вершины, с которыми данную вершину можно соединить цепью. Получим часть графа, которая и будет компонентой.

Определение 31. Сетью называется связный ориентированный граф без петель и циклов.

Вершины с полустепенью захода 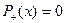, называются входами, и с полустепенью исхода , называются выходами.

Определение 32. Говорят, что дуга направлена от входа к выходу, если она лежит на некотором пути 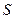от некоторого входа к некоторому выходу.

Теорема 5. Каждая сеть содержит как входы, так и выходы, причем каждая дуга сети ориентирована от входа к выходу.

Доказательство. Пусть 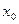- вершина сети. Либо 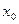- выход, либо существует такая вершина 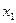и дуга 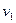, что 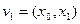. Либо 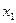- выход, либо существует такая вершина 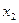и дуга 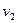, что , и т.д. В силу конечности графа получаем конечную цепочку вершин , которая обрывается на вершине , являющейся, очевидно, выходом. Аналогично доказывается существование хотя бы одного входа сети. Если 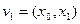- дуга сети, то от 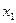начинается цепь, заканчивающаяся выходом и в 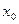заканчивается некоторая цепь, начинающаяся на входе. Таким образом, соединяя обе цепи дугой 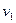получаем цепь от входа к выходу, содержащую 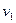. Теорема доказана.

Дата добавления: 2014-01-05