Критерии устойчивости Михайлова и Найквиста (частотные)

Частотные критерии устойчивости стационарных линейных систем были найдены Найквистом и Михайловым. Запишем характеристическое уравнение САУ при s = iw с целью его рассмотрения в частотной области:

B(iw) = b_n (iw)ⁿ + b_n-1 (iw)^n-1+...+ b_o = A (w) e ^{iY (w)} = P(w) + i Q(w) = 0.

При изменении w от 0 до ¥, вектор B(iw) начинает описывать в комплексной плоскости кривую, которую называют кривой Михайлова:

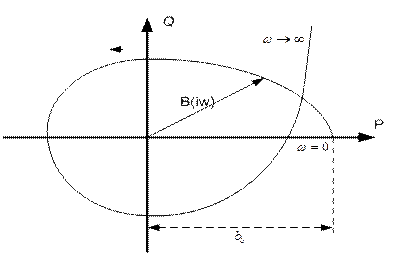
Рис. 1.19. Кривая Михайлова САУ

Михайлов доказал что, для того чтобы САУ была устойчива необходимо и достаточно, чтобы вектор кривой B(iw) при w = 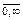повернулся, нигде не обращаясь в 0, вокруг начала координат против часовой стрелки на угол (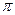n)/2, где n - степень характеристического уравнения. Отметим, что в неустойчивых системах нарушается последовательность прохождения кривой Михайлова квадрантов комплексной.

В 1932 году Найквистом был опубликован критерий, позволяющий судить об устойчивости замкнутой системы по амплитудно-фазовой характеристике Z( 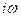) разомкнутой системы, что позволило значительно упростить расчеты. Примем во внимание тот факт, что если система управления в разомкнутом состоянии неустойчива, то ее характеристическое уравнение имеет k корней, лежащих в правой полуплоскости s. Рассмотрим функцию

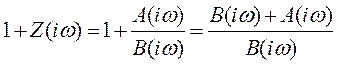
(1.31)

В числителе этой функции содержится характеристический полином замкнутой системы, в знаменателе – характеристический полином разомкнутой системы. Пусть степень полинома A(s) = a₀ s^m + a₁ s^m-1+...+ a_m

не выше степени n полинома B(s)= b₀ sⁿ + b₁ s^n-1+...+ b_{n .} Тогда степени числителя и знаменателя (2.1) одинаковы и равны n. В плоскости s функция 1+ Z(iw) изображается вектором, начало которого находится в точке (-1,0), а конец расположен на амплитудно-фазовой характеристике разомкнутой системы.

Для того, чтобы установившееся движение в замкнутой системе было устойчивым, необходимо и достаточно, чтобы при возрастании w от 0 до ¥ вектор 1+ Z(iw), скользящий своим концом по амплитудно – фазовой характеристике разомкнутой системы, повернулся вокруг точки (-1, 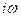) в направлении по часовой стрелке k /2 раз, где k – число правых корней характеристического уравнения разомкнутой системы. Под правыми корнями здесь понимаются корни, расположенные в правой полуплоскости комплексной плоскости s.

Дата добавления: 2014-01-05