
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод ложного положения
|
|
|
|
Метод секущих (метод хорд)
В этом и следующем разделе рассмотрим модификации метода Ньютона.
Как видно из формулы (2.13), метод Ньютона требует для своей реализации вычисления производной, что ограничивает его применение. Метод секущих лишен этого недостатка. Если производную заменить ее приближением:
f '(xn)» 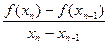 ,
,
то вместо формулы (2.13) получим
x n +1 = x n –. 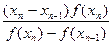 . (2.20)
. (2.20)
Это означает, что касательные заменены секущими. Метод секущих является двухшаговым методом, для вычисления приближения x n +1 необходимо вычислить два предыдущих приближения x n и x n – 1 , и, в частности, на первой итерации надо знать два начальных значения x 0 и x 1.
Формула (2.20) является расчетной формулой метода секущих. На рис. 2.9 приведена геометрическая иллюстрация метода секущих.

Рис. 2.9
Очередное приближение x n +1 получается как точка пересечения с осью OX секущей, соединяющей точки графика функции f (x) с координатами (x n -1, f (x n - 1)) и (x n , f (x n)).
Сходимость метода. Сходимость метода секущих устанавливает следующая теорема.
Теорема 2.4 Пусть x * – простой корень уравнения f (x) = 0, и в некоторой окрестности этого корня функция f дважды непрерывно дифференцируема, причем f" (x) ¹ 0. Тогда найдется такая малая s -окрестность корня x *, что при произвольном выборе начальных приближений x 0 и x 1 из этой окрестности итерационная последовательность, определенная по формуле (2.20) сходится и справедлива оценка:
| xn + 1 – x* | £ C | xn – x* | p, n ³ 0, p = 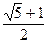 » 1.618. (2.21)
» 1.618. (2.21)
Сравнение оценок (2.15) и (2.21) показывает, что p < 2, и метод секущих сходится медленнее, чем метод Ньютона. Но в методе Ньютона на каждой итерации надо вычислять и функцию, и производную, а в методе секущих – только функцию. Поэтому при одинаковом объеме вычислений в методе секущих можно сделать примерно вдвое больше итераций и получить более высокую точность.
Так же, как и метод Ньютона, при неудачном выборе начальных приближений (вдали от корня) метод секущих может расходиться. Кроме того применение метода секущих осложняется из-за того, что в знаменатель расчетной формулы метода (2.20) входит разность значений функции. Вблизи корня эта разность мала, и метод теряет устойчивость.
Критерий окончания. Критерий окончания итераций метода секущих такой же, как и для метода Ньютона. При заданной точности e > 0 вычисления нужно вести до тех пор, пока не будет выполнено неравенство
| xn – xn – 1| < e. (2.22)
Пример 2.4.
Применим метод секущих для вычисления положительного корня уравнения 4(1 – x 2) – e x = 0 с точностью e = 10-3.
Корень этого уравнения находится на отрезке [0, 1], так как f (0) = 3 > 0, а f (1) = – e < 0. Подсчитаем вторую производную функции: f "(x) = – 8 – e x. Условие f (x) f " (x) ³ 0 выполняется для точки b = 1. В качестве начального приближения возьмем x 0 = b = 1. В качестве второго начального значения возьмем x 1 = 0.5. Проведем вычисления по расчетной формуле (2.20). Результаты приведены в табл. 2.4.
Таблица 2.4
| n | xn |
| 1.0000 0.5000 0.6660 0.7093 0.7033 0.7034 |
Рассмотрим еще одну модификацию метода Ньютона.
Пусть известно, что простой корень x * уравнения f (x) = 0 находится на отрезке [ a, b ] и на одном из концов отрезка выполняется условие f (x) f" (x) ³ 0. Возьмем эту точку в качестве начального приближения. Пусть для определенности это будет b. Положим x 0 = a. Будем проводить из точки B = (b, f (b)) прямые через расположенные на графике функции точки Bn с координатами (xn, f (xn), n = 0, 1, …. Абсцисса точки пересечения такой прямой с осью OX есть очередное приближение xn+ 1.
Геометрическая иллюстрация метода приведена на рис. 2.10.

Рис. 2.10
Прямые на этом рисунке заменяют касательные в методе Ньютона (рис. 2.8). Эта замена основана на приближенном равенстве
f '(xn)» 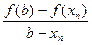 . (2.23)
. (2.23)
Заменим в расчетной формуле Ньютона (2.13) производную f '(xn) правой частью приближенного равенства (2.23). В результате получим расчетную формулу метода ложного положения:
x n +1 = x n –.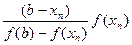 . (2.24)
. (2.24)
Метод ложного положения обладает только линейной сходимостью. Сходимость тем выше, чем меньше отрезок [ a, b ].
Критерий окончания. Критерий окончания итераций метода ложного положения такой же, как и для метода Ньютона. При заданной точности e > 0 вычисления нужно вести до тех пор, пока не будет выполнено неравенство
| xn – xn – 1| < e. (2.25)
Пример 2.5.
Применим метод ложного положения для вычисления корня уравнения x 3 + 2 x – 11 = 0 с точностью e = 10-3.
Корень этого уравнения находится на отрезке [1, 2], так как f (1) = –8 < 0, а f (2) = 1 > 0. Для ускорения сходимости возьмем более узкий отрезок [1.9, 2], поскольку f (1.9) < 0, а f (2) > 0. Вторая производная функции f (x) = x 3 + 2 x – 11 равна 6 x. Условие f (x) f" (x) ³ 0 выполняется для точки b = 2. В качестве начального приближения возьмем x 0 = a = 1.9. По формуле (2.24) имеем
x 1 = x 0 –.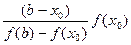 = 1.9 +
= 1.9 + 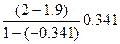 » 1.9254.
» 1.9254.
Продолжая итерационный процесс, получим результаты, приведенные в табл. 2.5.
Таблица 2.5
| n | xn |
| 1.9 1.9254 1.9263 1.9263 |
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 5707; Нарушение авторских прав?; Мы поможем в написании вашей работы!