
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод исключения Гаусса с выбором главного элемента по столбцу
|
|
|
|
Метод исключения Гаусса. Схема единственного деления
Основная идея метода исключений Гаусса состоит в том, что система уравнений (3.1) приводится к эквивалентной ей системе с верхней треугольной матрицей (прямой ход исключений), а затем неизвестные вычисляются последовательной подстановкой (обратный ход исключений).
Рассмотрим сначала простейший метод исключения Гаусса, называемый схемой единственного деления.
Прямой ход состоит из n – 1 шагов. На первом шаге исключается переменная x 1 из всех уравнений, кроме первого. Для этого нужно из второго, третьего, …, n- го уравнений вычесть первое, умноженное на величину
m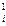 =
= 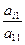 , i = 2, 3, …, n. (3.4)
, i = 2, 3, …, n. (3.4)
При этом коэффициенты при x 1 обратятся в нуль во всех уравнениях, кроме первого.
Введем обозначения:
a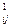 = aij – m
= aij – m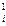 a 1 j , b
a 1 j , b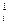 = bi – m
= bi – m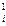 b 1. (3.5)
b 1. (3.5)
Легко убедиться, что для всех уравнений, начиная со второго, a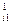 = 0, i = 2, 3, …, n. Преобразованная система запишется в виде:
= 0, i = 2, 3, …, n. Преобразованная система запишется в виде:
 a 11 x 1 + a 12 x 2 + a 13 x 3 + … + a 1 n xn = b 1
a 11 x 1 + a 12 x 2 + a 13 x 3 + … + a 1 n xn = b 1
a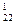 x 2 + a
x 2 + a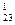 x 3 + … + a
x 3 + … + a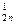 xn = b
xn = b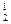
a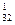 x 2 + a
x 2 + a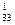 x 3 + … + a
x 3 + … + a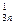 xn = b
xn = b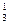 (3.6)
(3.6)
a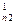 x 2 + a
x 2 + a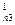 x 3 + … + a
x 3 + … + a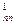 xn = b
xn = b
Все уравнения (3.6), кроме первого, образуют систему (n – 1)-го порядка. Применяя к ней ту же процедуру, мы можем исключить из третьего, четвертого, …, n- го уравнений переменную x 2. Точно так же исключаем переменную x 3 из последних n – 3 уравнений.
На некотором k -ом шаге в предположении, что главный элемент k-ого шага a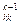
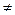 0, переменная x k исключается с помощью формул:
0, переменная x k исключается с помощью формул:
m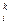 =
= 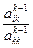 ,
,
a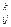 = a
= a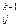 – m
– m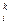 a
a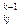 ,
,
b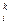 = b
= b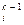 – m
– m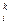 b
b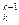 , i, j = k + 1, k + 2, …, n. (3.7)
, i, j = k + 1, k + 2, …, n. (3.7)
Индекс k принимает значения 1, 2, …, n – 1.
При k = n – 1 получим треугольную систему:
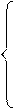 a 11 x 1 + a 12 x 2 + a 13 x 3 + … + a 1 n xn = b 1
a 11 x 1 + a 12 x 2 + a 13 x 3 + … + a 1 n xn = b 1
a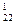 x 2 + a
x 2 + a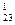 x 3 + …+ a
x 3 + …+ a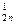 xn = b
xn = b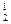
a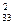 x 3 + …+ a
x 3 + …+ a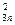 xn = b
xn = b (3.8)
(3.8)
a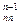 xn = b
xn = b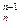
с треугольной матрицей An.
Приведение системы (3.1) к треугольному виду (3.8) составляет прямой ход метода Гаусса.
При использовании метода Гаусса нет необходимости в предварительном обосновании существования и единственности решения (т. е. доказательства, что det A ¹ 0). Если на k -ом шаге все элементы a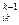 (i = k, k + 1, …, n) окажутся равными нулю, то система (3.1) не имеет единственного решения.
(i = k, k + 1, …, n) окажутся равными нулю, то система (3.1) не имеет единственного решения.
Обратный ход состоит в вычислении переменных. Из последнего уравнения (3.8) определяем xn ... Подставляя его в предпоследнее уравнение, находим xn- 1, и т. д. Общие формулы имеют вид:
xn = 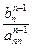 ,
,
xk = 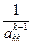 (b
(b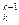 - a
- a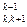 xk+ 1 - a
xk+ 1 - a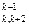 xk+ 2 - … - a
xk+ 2 - … - a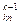 xn), k = n – 1, n – 2, …, 1 (3.9)
xn), k = n – 1, n – 2, …, 1 (3.9)
Трудоемкость метода. Для реализации метода исключения Гаусса требуется примерно 2/3 n 3 операций для прямого хода и n 2 операций для обратного хода. Таким образом, общее количество операций составляет примерно 2/3 n 3 + n 2.
Пример 3.1.
Применим метод исключения Гаусса по схеме единственного деления для решения системы уравнений:
 2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
0.4 x 1 + 0.5 x 2 + 4.0 x 3 – 8.5 x 4 = 21.9
0.3 x 1 – 1.0 x 2 + 1.0 x 3 + 5.2 x 4 = – 3.9 (3.10)
1.0 x 1 + 0.2 x 2 + 2.5 x 3 – 1.0 x 4 = 9.9
Будем делать округление чисел до четырех знаков после десятичной точки.
Прямой ход. 1-ый шаг. Вычислим множители:
m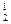
 =
= 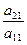 =
= 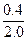 = 0.2; m
= 0.2; m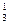 =
= 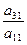 =
= 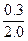 = 0.15; m
= 0.15; m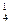 =
= 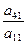 =
= 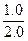 = 0.5.
= 0.5.
Вычитая из второго, третьего и четвертого уравнений системы (3.10) первое уравнение, умноженное соответственно на m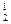 , m
, m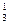 , m
, m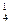 , получим новую систему:
, получим новую систему:
 2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
0.3 x 2 + 4.02 x 3 – 8.70 x 4 = 21.36
– 1.15 x 2 + 1.015 x 3 + 5.05 x 4 = – 4.305 (3. 11)
– 0.30 x 2 + 2.55 x 3 – 1.50 x 4 = 8.55
2-ой шаг. Вычислим множители:
m =
= 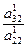 =
= 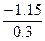 = – 3.83333; m
= – 3.83333; m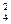 =
=  =
= 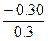 = –1.0.
= –1.0.
Вычитая из третьего и четвертого уравнений системы (3.11) второе уравнение, умноженное соответственно на m и m
и m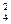 , приходим к системе:
, приходим к системе:
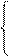 2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
0.3 x 2 + 4.02 x 3 – 8.70 x 4 = 21.36
16. 425 x 3 – 28.300 x 4 = 77. 575 (3.12)
6.570 x 3 – 10.200 x 4 = 29.910
3-ий шаг. Вычислим множитель:
m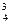 =
= 
 =
= 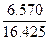 = 0.4.
= 0.4.
Вычитая из четвертого уравнения системы (3.12) третье, умноженное на m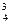 , приведем систему к треугольному виду:
, приведем систему к треугольному виду:
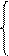 2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
0.3 x 2 + 4.02 x 3 – 8.70 x 4 = 21.36
16. 425 x 3 – 28.300 x 4 = 77. 575 (3.13)
1.12 x 4 = – 1.12
Обратный ход. Из последнего уравнения системы (3.13) находим x 4 = 1.000. Подставляя значение x 4 в третье уравнение, получим x 3 = 2.000. Подставляя найденные значения x 4 и x 3 во второе уравнение, найдем x 2 = 3.000. Наконец, из первого уравнения, подставив в него найденные значения x 4, x 3 и x 2, вычислим x 1 = – 1.000.
Итак система (3.10) имеет следующее решение:
x 1 = 1.000, x 2 = 2.000, x 3 = 3.000, x 4 = – 1.000.
Хотя метод Гаусса является точным методом, ошибки округления могут привести к существенным погрешностям результата. Кроме того исключение по формулам (3.7) нельзя проводить, если элемент главной диагонали a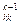 равен нулю. Если элемент a
равен нулю. Если элемент a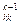 мал, то велики ошибки округления при делении на этот элемент. Для уменьшения ошибок округления применяют метод исключения Гаусса с выбором главного элемента по столбцу. Прямой ход так же, как и для схемы единственного деления, состоит из n – 1 шагов. На первом шаге прежде, чем исключать переменную x 1, уравнения переставляются так, чтобы в левом верхнем углу был наибольший по модулю коэффициент ai 1, i = 1, 2, …, n. В дальнейшем, на k -м шаге, прежде, чем исключать переменную xk, уравнения переставляются так, чтобы в левом верхнем углу был наибольший по модулю коэффициент aik, i = k, k + 1, …, n. После этой перестановки исключение переменной xk производят, как в схеме единственного деления.
мал, то велики ошибки округления при делении на этот элемент. Для уменьшения ошибок округления применяют метод исключения Гаусса с выбором главного элемента по столбцу. Прямой ход так же, как и для схемы единственного деления, состоит из n – 1 шагов. На первом шаге прежде, чем исключать переменную x 1, уравнения переставляются так, чтобы в левом верхнем углу был наибольший по модулю коэффициент ai 1, i = 1, 2, …, n. В дальнейшем, на k -м шаге, прежде, чем исключать переменную xk, уравнения переставляются так, чтобы в левом верхнем углу был наибольший по модулю коэффициент aik, i = k, k + 1, …, n. После этой перестановки исключение переменной xk производят, как в схеме единственного деления.
Трудоемкость метода. Дополнительные действия по выбору главных элементов требуют примерно n 2 операций, что практически не влияет на общую трудоемкость метода.
Пример 3.2.
Применим метод исключения Гаусса с выбором главного элемента по столбцу для решения системы уравнений (3.10) из примера 3.1. Прямой ход. 1-ый шаг. Так как коэффициент a 11 = 2.0 наибольший из коэффициентов первого столбца, перестановки строк не требуется и 1-ый шаг полностью совпадает с 1-ым шагом примера 3.1. Из второго, третьего и четвертого уравнений исключается переменная x 1 и система приводится к виду (3.11).
2-ой шаг. Наибольший по модулю коэффициент при x 2 в системе (3.11) a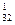 = – 1.15. Поэтому переставим уравнения следующим образом:
= – 1.15. Поэтому переставим уравнения следующим образом:
 2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
– 1.15 x 2 + 1.015 x 3 + 5.05 x 4 = – 4.305 (3.14)
0.3 x 2 + 4.02 x 3 – 8.70 x 4 = 21.36
– 0.30 x 2 + 2.55 x 3 – 1.50 x 4 = 8.55
Вычислим множители:
m =
= 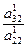 =
= 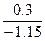 = –0.26087 m
= –0.26087 m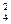 =
=  =
= 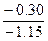 = 0.26087.
= 0.26087.
Вычитая из третьего и четвертого уравнений системы (3.14) второе уравнение, умноженное соответственно на m и m
и m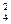 , приходим к системе:
, приходим к системе:
 2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
– 1.15 x 2 + 1.015 x 3 + 5.05 x 4 = – 4.305 (3.15)
4.28478 x 3 – 7. 38261 x 4 = 20.23696
2.28522 x 3 – 2.81739 x 4 = 9.67305
3-ий шаг. Вычислим множитель:
m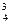 =
= 
 =
= 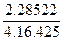 = 0.53333.
= 0.53333.
Вычитая из четвертого уравнения системы (3.15) третье, умноженное на m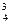 , приведем систему к треугольному виду:
, приведем систему к треугольному виду:
 2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
2.0 x 1 + 1.0 x 2 – 0.1 x 3 + 1.0 x 4 = 2.7
– 1.15 x 2 + 1.015 x 3 + 5.05 x 4 = – 4.305 (3.16)
4.28478 x 3 – 7. 38261 x 4 = 20.23696
1.11998 x 4 = – 1.11998
Обратный ход. Обратный ход полностью совпадает с обратным ходом примера 3.1. Решение системы имеет вид:
x 1 = 1.000, x 2 = 2.000, x 3 = 3.000, x 4 = – 1.000.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 809; Нарушение авторских прав?; Мы поможем в написании вашей работы!