
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модифицированные методы Эйлера
|
|
|
|
Первый модифицированный метод Эйлера. Суть этого метода состоит в следующем. Сначала вычисляются вспомогательные значения искомой функции y в точках t
в точках t = ti +
= ti +  с помощью формулы:
с помощью формулы:
y = yi +
= yi +  fi = yi +
fi = yi + f (ti, yi).
f (ti, yi).
Затем находится значение правой части уравнения (6.1) в средней точке
f = f (t
= f (t , y
, y )
)
и затем полагается
yi+ 1 = yi + h f , i = 0, 1, …, n – 1. (6.12)
, i = 0, 1, …, n – 1. (6.12)
Формулы (6.12) являются расчетными формулами первого модифицированного метода Эйлера.
Первый модифицированный метод Эйлера является одношаговым методом со вторым порядком точности
Второй модифицированный метод Эйлера – Коши. Суть этого метода состоит в следующем. Сначала вычисляются вспомогательные значения
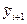 = yi + h f (ti, yi). (6.13)
= yi + h f (ti, yi). (6.13)
Затем приближения искомого решения находятся по формуле:
yi+ 1 = yi +  [ f (ti, yi) + f (ti+ 1,
[ f (ti, yi) + f (ti+ 1, 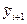 )], i = 0, 1, …, n – 1. (6.14)
)], i = 0, 1, …, n – 1. (6.14)
Формулы (6.14) являются расчетными формулами второго модифицированного метода Эйлера – Коши.
Второй модифицированный метод Эйлера – Коши, так же, как и первый, является одношаговым методом со вторым порядком точности.
Оценка погрешности. Приближенная оценка погрешности модифицированных методов Эйлера осуществляется как и для простого метода Эйлера с использованием правила Рунге (см. предыдущий раздел 6.2). Так как оба модифицированных метода Эйлера имеют второй порядок точности, т. е. p = 2, то оценка погрешности (6.6) примет вид
R» 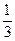 | y
| y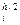 - y
- y |. (6.15)
|. (6.15)
Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши модифицированными методами Эйлера с заданной точностью e. Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение y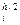 , i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие:
, i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие:
R» 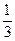 | y
| y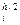 - y
- y | < e. (6.16)
| < e. (6.16)
Приближенным решением будут значения y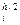 , i = 0, 1, …, n.
, i = 0, 1, …, n.
Пример 6.2.
Применим первый модифицированный метод Эйлера для решения задачи Коши
y' (t) = y –  , y (0) = 1,
, y (0) = 1,
рассмотренной ранее в примере 6.1.
Возьмем шаг h = 0.2. Тогда n =  = 5.
= 5.
В соответствии с (6.3) получим расчетную формулу первого модифицированного метода Эйлера:
yi+ 1 = yi + h f = yi + 0.2 f
= yi + 0.2 f , где
, где
f = f (t
= f (t , y
, y ) = y
) = y –
–  ,
,
t = ti +
= ti +  = ti + 0.1,
= ti + 0.1,
y = yi +
= yi + f (ti, yi) = yi +0.1
f (ti, yi) = yi +0.1 ,
,
t0 = 0, y0 = 1, i = 0, 1, …, 4.
Решение представим в виде таблицы 6.3:
Таблица 6.3
| i | ti | yi |  f (ti, yi) f (ti, yi)
| t
| y
| h f
|
| 0.2 0.4 0.6 0.8 1.0 | 1.1836 1.3426 1.4850 1.6152 1.7362 | 0.1 0.0850 0.0747 0.0677 0.0625 | 0.1 0.3 0.5 0.7 0.9 | 1.1 1.2682 1.4173 1.5527 1.6777 | 0.1836 0.1590 0.1424 0.1302 0.1210 |
Третий столбец таблицы 6.3 содержит приближенное решение yi, i = 0, 1, …, 5.
Сравним полученное приближенное решение с точным решением (6.11), представленном в таблице 6.2. Виднм, что погрешность составляет R = 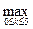 | y (ti) – yi | = 0.0042.
| y (ti) – yi | = 0.0042.
Пример 6.3.
Применим второй модифицированный метод Эйлера – Коши для решения задачи Коши
y' (t) = y –  , y (0) = 1,
, y (0) = 1,
рассмотренной ранее в примерах 6.1 и 6.2. Так же, как и ранее, зададим шаг h = 0.2. Тогда n =  = 5.
= 5.
В соответствии с (6.14) получим расчетную формулу метода Эйлера – Коши:
yi+ 1 = yi +  [ f (ti, yi) + f (ti+ 1,
[ f (ti, yi) + f (ti+ 1, 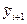 )] = yi + 0.1[ f (ti, yi) + f (ti+ 1,
)] = yi + 0.1[ f (ti, yi) + f (ti+ 1, 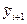 )],
)],
где
f (ti, yi) = yi – 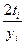
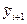 = yi + h f (ti, yi) = yi + 0.1
= yi + h f (ti, yi) = yi + 0.1
t0 = 0, y0 = 1, i = 0, 1, …, 4.
Решение представим в виде таблицы 6.4:
Таблица 6.4
| i | ti | yi |  f (ti, yi) f (ti, yi)
| ti+ 1 | 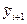
| f (ti+ 1, 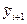 ) )
|
| 0.2 0.4 0.6 0.8 1.0 | 1.1867 1.3484 1.4938 1.6272 1.7542 | 0.1 0.0850 0.0755 0.0690 0.0645 | 0.2 0.4 0.6 0.8 1.0 | 1.2 1.3566 1.4993 1.6180 1.7569 | 0.867 0.767 0.699 0.651 0.618 |
Таблица 6.4 заполняется последовательно по строкам, сначала первая строка, затем вторая и т. д. Третий столбец таблицы 6.4 содержит приближенное решение yi, i = 0, 1, …, 5.
Сравним полученное приближенное решение с точным решением (6.11), представленном в таблице 6.2. Видим, что погрешность составляет R = 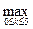 | y (ti) – yi | = 0.0222.
| y (ti) – yi | = 0.0222.
6.4 Метод Рунге – Кутта
Метод Рунге – Кутта является одним из наиболее употребительных методов высокой точности. Метод Эйлера можно рассматривать как простейший вариант метода Рунге – Кутта.
Рассмотрим задачу Коши для дифференциального уравнения
y' (t) = f (t, y (t))
с начальным условием y (t 0 ) = y 0.
Как и в методе Эйлера, выберем шаг h =  и построим сетку с системой узлов ti = t 0 + ih, i = 0, 1, …, n.
и построим сетку с системой узлов ti = t 0 + ih, i = 0, 1, …, n.
Обозначим через yi приближенное значение искомого решения в точке ti.
Приведем расчетные формулы метода Рунге – Кутта четвертого порядка точности:
yi+ 1 = yi + 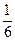 h (k
h (k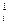 + 2 k
+ 2 k + 2 k
+ 2 k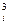 + k
+ k ),
),
k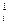 = f (ti, yi),
= f (ti, yi),
k = f (ti +
= f (ti +  , yi +
, yi +  k
k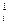 ), (6.17)
), (6.17)
k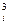 = f (ti +
= f (ti +  , yi +
, yi +  k
k ),
),
k = f (ti + h, yi + hk
= f (ti + h, yi + hk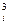 ),
),
i = 0, 1, …, n.
Оценка погрешности. О ценка погрешности метода Рунге – Кутта затруднительна. Грубую оценку погрешности дает правило Рунге (см. раздел 6.2). Так как метод Рунге - Кутта имеет четвертый порядок точности, т. е. p = 4, то оценка погрешности (6.6) примет вид
R»  | y
| y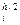 - y
- y |. (6.18)
|. (6.18)
Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши методом Рунге – Кутта четвертого порядка точности с заданной точностью e. Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение y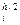 , i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие:
, i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие:
R»  | y
| y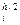 - y
- y | < e. (6.19)
| < e. (6.19)
Приближенным решением будут значения y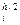 , i = 0, 1, …, n.
, i = 0, 1, …, n.
Пример 6.4.
Методом Рунге – Кутта четвертого порядка точности найдем решение на отрезке [0, 1] следующей задачи Коши.
y' (t) = 2ty, y (0) = 1. (6.20)
Возьмем шаг h = 0.1. Тогда n = 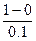 = 10.
= 10.
В соответствии с (6.17) расчетные формулы примут вид:
yi+ 1 = yi + 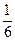 h (k
h (k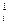 + 2 k
+ 2 k + 2 k
+ 2 k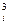 + k
+ k ),
),
k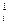 = 2 tiyi,
= 2 tiyi,
k = 2(ti +
= 2(ti +  )(yi +
)(yi +  k
k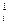 ), (6.21)
), (6.21)
k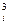 = 2(ti +
= 2(ti +  )(yi +
)(yi +  k
k ),
),
k = 2(ti + h)(yi + hk
= 2(ti + h)(yi + hk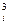 ),
),
i = 0, 1, …, 10.
Задача (6.20) имеет точное решение: y (t) = e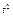 , поэтому погрешность определяется как абсолютная величина разности между точными и приближенными значениями ei = | y (ti) – yi |.
, поэтому погрешность определяется как абсолютная величина разности между точными и приближенными значениями ei = | y (ti) – yi |.
Найденные по формулам (6.21) приближенные значения решения yi и их погрешности ei представлены в таблице 6.5:
Таблица 6.5
| ti | yi | ei | ti | yi | ei |
| 0.1 0.2 0.3 0.4 0.5 | 1.01005 1.04081 1.09417 1.17351 1.28403 | 10-9 4×10-9 2×10-8 6×10-8 2×10-7 | 0.6 0.7 0.8 0.9 1.0 | 1.43333 1.63232 1.89648 2.24790 2.71827 | 5×10-7 2×10-6 3×10-6 6×10-6 2×10-5 |
Задачи к зачету по курсу “Вычислительные методы”
Указание. Каждый студент вначале должен определить параметр своего контрольного задания, s = log10(1 + ), где k - номер студента в списке группы, k = 1, 2, … Решение задач должно быть оформлено аккуратно и содержать все промежуточные расчеты. В качестве образца можно взять примеры, рассмотренные в соответствующих разделах методических указаний.
), где k - номер студента в списке группы, k = 1, 2, … Решение задач должно быть оформлено аккуратно и содержать все промежуточные расчеты. В качестве образца можно взять примеры, рассмотренные в соответствующих разделах методических указаний.
1. Методом деления отрезка пополам найти корень уравнения
4(1 – x 2) – ex = s с точностью e = 10-3.
2. Методом Зейделя решить систему уравнений с точностью e =10-3.
 |
 6.2+ s 2.2+ s 1.2+ s 16.55+ s
6.2+ s 2.2+ s 1.2+ s 16.55+ s
A = 2.2+ s 5.5+ s -1.5+ s, b = 10.55+ s.
1.2+ s -1.5+ s 7.2 + s 16.80+ s
3. Найти приближение функции f (x) = esx на отрезке [0, 1] многочленом Тейлора с точностью e = 10-3 . Вычислить es.
4. Вычислить приближенно по формуле средних прямоугольников интеграл  при n = 4 и оценить погрешность результата.
при n = 4 и оценить погрешность результата.
5. Методом Эйлера найти численное решение задачи Коши
y ' = 2 sy; y (0) = 1, на отрезке [0, 1] с шагом h = 0.2.
Сравнить с точным решением.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1982; Нарушение авторских прав?; Мы поможем в написании вашей работы!