
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правило произведения. Если элемент A можно выбрать n способами из указанного множества, и после этого элемент B может быть выбран m способами
|
|
|
|
Если элемент A можно выбрать n способами из указанного множества, и после этого элемент B может быть выбран m способами, то выбор пары А и В может быть сделан (n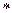 m) способами.
m) способами.
Пример 3:
В книжном шкафу на двух полках стоят книги. На первой полке – 5 книг, а на второй – 10. Сколькими способами можно выбрать одну книгу с первой полки и одну со второй?
Решение: Книгу с первой полки можно выбрать 5-ю способами, т.е. n=5, книгу со второй полки можно выбрать 10-ю способами, т.е. m=10. Для ответа на вопрос задачи воспользуемся правилом произведения.
5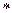 10=50 способов.
10=50 способов.
Пример 4:
В лотерее каждому участнику даётся трёхзначный номер от 000 до 999. Организаторы лотереи решили, что выигрышными будут те номера, в которых есть хоть одна восьмерка. Сколько будет невыигрышных номеров?
Решение:
Первую цифру числа можно записать 9-ю способами, т.к. без восьмёрки 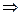 n=9. Вторую и третью цифры числа можно также записать 9-ю способами
n=9. Вторую и третью цифры числа можно также записать 9-ю способами 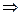 m=9, k=9. Воспользуемся правилом произведения
m=9, k=9. Воспользуемся правилом произведения
m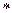 n
n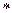 k=9
k=9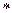 9
9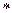 9=729 проигрышных номеров.
9=729 проигрышных номеров.
Пример 5:
В букинистическом магазине лежат 6 разных изданий романа И.С. Тургенева «Рудин», три издания его же романа «Дворянское гнездо» и четыре издания романа «Отцы и дети». Кроме того, есть 5 разных сборников, в каждом из которых есть романы «Рудин» и «Дворянское гнездо», и 7 сборников с романами «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно сделать покупку, содержащую по одному экземпляру каждого из этих романов?
Решение:
Рудин – 6.
Дв. гнездо – 3
От. и дети – 4
 - 5 изд
- 5 изд
 - 7 изд.
- 7 изд.
Воспользуемся правилами суммы и произведения:
6∙3∙4 + 5∙4 + 6∙7=72+20+42=134
Перед изучение следующей темы, повторим со школы теорию вероятности, ее формулы, повторим что такое факториал, как его находить и где применять. И так записываем следующую тему:
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1733; Нарушение авторских прав?; Мы поможем в написании вашей работы!