Свойства сочетаний

ü , если n<k или k<0;

ü , ;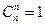

ü ;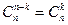

ü Рекуррентная формула (выражает следующее через предыдущее)

,

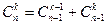Задания записывают в тетрадь, затем далось 20 мин., для самостоятельной работы. Далее каждую задачу разобрали у доски до полного усвоения материала, студенты выходили к доске и объясняли какдый ход решения, что и от куда взяли и почему такой ответ.

Задания

1. Имеются 5 красок. Сколько существует способов для

а) выбора трех красок;

б) раскрашивания трехцветного полосатого флага с заданным направлением полос;

в) для раскрашивания трехцветного флага с заданным направлением полос, если одна полоса должна быть красной?

Решение:

а) Находим число сочетаний из 5 по 3 (т.к. порядок не важен)

способов.

б) Находим число размещений из 5 по 3 (т.к. важен порядок)

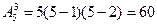способов

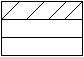
в)

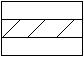или или

Находим в каждом случае число размещений из 4 цветов (т.к. пятый уже занят – красный) по 2 (т.к. цвет третьей полосы уже известен). А затем сложим их.

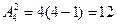способов в каждом случае.

12+12+12=36 способов.

2. В группе 7 юношей и 5 девушек. Сколько существует способов для выбора 6 человек, чтобы среди них было не менее 4-х юношей.

Решение:

ю ю ю ю д д или

ю ю ю ю ю д или

ю ю ю ю ю ю

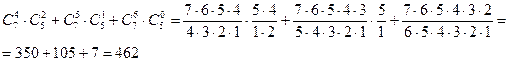
3. Среди 10 команд разыгрывается 3 комплекта медалей: золото, серебро, бронза. Сколько существует способов распределения?

Решение:

Находим число размещений из 10 по 3 (т.к. важен порядок):

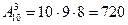
Начало второй пары, знакомство с понятие Бином Ньютона.

Записывается формула с полным пояснением,.

Дата добавления: 2014-01-05