Сочетания с повторением

Перестановки с повторением

Множество состоит из n элементов. Порядок расположения элементов важен.

n₁ – элементы первого типа

n₂ – элементы второго типа

................................................

n_k – элементы k - ого типа

всего n элементов.

n₁+ n₂ +...+n_k= n

Тогда число различных перестановок из этих элементов:

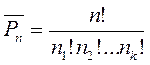
Пример:

Сколько слов можно составить из букв: А, А, М, М?

Решение: n=4, n₁ – 2 буквы А, n₂ – 2 буквы М

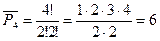способов

( Каждая формула и определение записывается и выделяется, для самостоятельного повторения изученного дома. )

Пусть имеются элементы n типов и из множества этих элементов выбирается k элементов, могут присутствовать элементы одного типа.

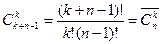- число сочетаний с повторением.

Разбор примеров, совместная беседа и работа студентов у доски.

Пример:

В кондитерской имеются пирожные четырех типов. Нужно взять 11 пирожных разного типа

Решение:

n=4, n₁ – наполеон, n₂ – картошка, n₃ - эклер, n₄ - медовое

k=11 5 3 2 1

4 1 6 0

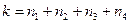
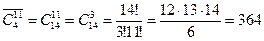
Примеры:

1. Сколько пятизначных номеров можно составить из девяти цифр 1, 2, 3, 4, 5, 6, 7, 8, 9?

Решение: Такие номера длиной 5, составленные из элементов множества из 9 элементов.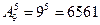

2. Сколькими способами можно переставить буквы в слове СТАТИСТИКА?

Решение: n=10, n₁ =2 (буква А встречается 2 раза), n₂ =2 (С), n₃=3 (Т), n₄=2 (И), n₅=1 (К)

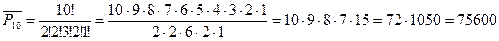
3. Сколько существует треугольников, у которых длина каждой стороны принимает одно из значений 4, 5, 6, 7?

Решение: k=3(3стороны), n=4 (4 значения)

Находим сочетания с повторением:

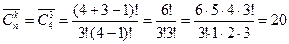
4. Лифт останавливается на 10 этажах. Сколькими способами можно распределить между этими остановками 8 человек.

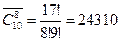
5. Сколько различных «слов» в 5 букв можно составить из 26 букв латинского алфавита.

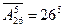
Домашнее задание:

1. Доказать рекуррентную формулу:

,

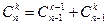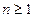
2. Используя Бином Ньютона получить формулы сокращенного умножения:

1)

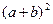
2)

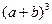
3)

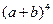
4)

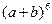
3. Сколько «слов» можно получить из букв слова МАТЕМАТИКА (в каждом слове все буквы).

4. Сколькими способами можно переставить буквы слова «перешеек» так, чтобы 4 буквы «е» не шли подряд?

Решение: Найдем все случаи перестановок

n=8, n₁=4(e)

Найдем случаи перестановок, когда 4 буквы «е» идут подряд.

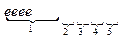
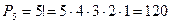
1680-120=1560 способов, когда 4 буквы «е» не идут подряд.

5. Для автомобильных номеров используют 10 цифр и 28 букв, каждый номер состоит из 3 букв и 4 цифр. Какое число машин можно пронумеровать? (номеров с 4-мя нулями быть не должно).

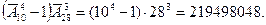
Опрос по изученному материалу (на отдельных листочках)

1) Написать формулы правила суммы и произведения;

2) Дать определение размещения,

3) Дать определение слову перестановка.

4) Записать формулу числа перестановок, написать формулы числа перестановок из n по m.

5) Написать формулу числа сочетаний с повторением.

Дата добавления: 2014-01-05