План лекции. Лекция 1. Матрицы и определители

Лекция 1. Матрицы и определители

ЛИНЕЙНАЯ АЛГЕБРА

Функции одной переменной

Дифференциальное исчисление

Аналитическая геометрия

Линейная алгебра

Курс лекций по высшей математике

для студентов инженерно-технических

специальностей

1.1. Основные сведения о матрицах

1.2. Oперации над матрицами

1.3. Oпределители квадратных матриц

1.4. Обратная матрица

1.5. Ранг матрицы

1.1. Основные сведения о матрицах

Определение 1. Матрица размера m ´ n – это прямоугольная таблица чисел, содержащая m строк и n столбцов.

Числа, составляющие матрицу, называются ее элементами.

Обозначения:

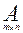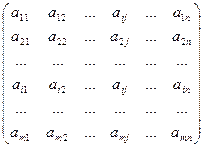= , А=(а_ij). i =, j =.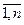

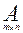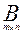
=а_ij = в _ij для i =, j =.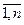

А=(а₁₁ а₁₂ … а_ij … а_1n) - матрица – строка; В=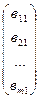- матрица-столбец.

Если m=n, то получаем квадратную матрицу порядка n: А=(а_ij)₁ⁿ

Элементы матрицы а_ij,у которой i=j, называются диагональными и образуют главную диагональ матрицы. Если А – квадратная матрица порядка n, то её главную диагональ образуют элементы а_11,а_22, а_{33, ….,}а_nn.

Диагональная матрица – квадратная матрица А, у которой все недиагональные элементы равны нулю.

Например, матрица А= есть диагональная матрица третьего порядка. Если у диагональной матрицы порядка n, все диагональные элементы равны 1, то получаем единичную матрицу Е.

Например, Е=- единичная матрица второго порядка.

Матрица любого размера называется нулевой, если все ее элементы нули. Обозначение О.

Всякую таблицу чисел, имеющую m строк и n столбцов, не меняя существа дела, можно записать, заменив строки столбцами и соответственно столбцы строками. В результате таблица будет содержать n строк и m столбцов.

После такого преобразования матрица А запишется как

=

Определение 2. Преобразование матрицы, заключающееся в замене ее строк столбцами (столбцов строками), называется транспонированием и обозначается индексом «Т» сверху. Следовательно, В = А^Т, А = В^Т.

Порядок матрицы при транспонировании изменяется на обратный: m x n на n x m. Очевидно, что двукратное транспонирование не меняет вида матрицы: (А^Т)^Т = А. Матрица–строка при транспонировании переходит в матрицу–столбец, матрица–столбец – в матрицу-строку.

Определение 3. Квадратная матрица, сохраняющая свой вид при транспонировании, называется симметричной (или симметрической).

Для симметрической матрицы справедливо равенство А^Т = А.

Нетрудно заметить, что в симметрической матрице элементы, расположенные симметрично относительно главной диагонали, одинаковы, то есть а_ij = а_ji при i ≠ j.

Симметрической является, например, любая диагональная матрица.

Квадратная матрица А называется кососимметричной, если она отвечает условию А^T =-А. Из этого условия находим, что главные диагональные элементы кососимметричной матрицы равны нулю, а элементы, симметричные относительно главной диагонали, отличаются лишь знаком. Например, кососимметричныеми являются матрицы:

А = , В = .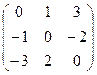

1.2. Oперации над матрицами

Определение 1. Произведением матрицы А на число λ называется матрица В = λ А, элементы которой в_ij = λ а_ij для i =, j =.

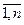Например, если А = , то 3А = .

Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.

Например, = 4 х .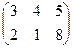

В частности, о ´ А = о.

Определение 2. Суммой двух матриц А и В одинакового размера m x n

называется матрица С = А + В, элементы которой С_{ij =} a_ij + b_ij для i =, j =.

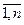Например, если А = , В =,

то С = А + В == .

В частности, А + О = А, А – В = А + (-1) В.

Определение 3. Умножение матрицы А на матрицу В определено, когда число столбцов матрицы А равно числу строк матрицы В (в частности, умножение всегда возможно, когда оба сомножителя – квадратные матрицы одного порядка). Тогда произведением матриц =называется такая матрица, каждый элемент которой С_ij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В, т.е. С_ij = a_i1b_1j+ a_i2b_2j + … + a_ikb_kj.

Например, если = , = 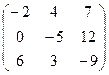, то

= = .

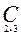Свойства операций над матрицами:

1) А + В = В + А (переместительное свойство);

2) (А + В) + С = А + (В + С) (сочетательное свойство);

3) λ(А+ В) = λА + λВ; (λ + μ)А = λА + μА; (λμ)А = λ(μА);

4) А(В + С) = АВ + АС;

5) (А + В)С = АС + ВС;

6) λ(АВ) = (λА)В = А (λВ);

7) А (В С) = (А В) С (сочетательный закон).

Свойства 1) - 7) вытекают из определений операций над матрицами и соответствующих свойств чисел.

8) АВ ≠ ВА (но АЕ = ЕА = А) – (специфическое свойство). Если АВ=ВА, то матрицы А и В называются перестановочными.

9) Из АВ = О не следует, что А=О или В=О. (специфическое свойство).

Например, если А = , В = , то АВ = О, но А ≠ О, В ≠ О.

Определение 4. Целой положительной степенью А^m(m>1) квадратной матрицы А называется произведение m матриц, равных А, т.е. А^m = .

При этом А⁰ = Е, А^/ = А, А^m А^k = А^m+k, (А^m)^k = А^mk.

Например, если А = ,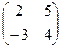

то А² = А А = 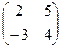x= .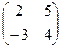

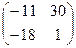Из равенства А^m= О еще не следует, что А = О.

Свойства операции транспонирования:

1) (λА)^T = λА^T;

2) (А + В)^T = А^T + В^T;

3) (А В)^T = В^TА^T.

1.3. Oпределители квадратных матриц.

Определение 1. Всякой квадратной матрице можно поставить в соответствие вещественное число, называемое определителем или детерминантом этой матрицы.

Обозначение: = Δ = detA = 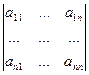. Элементы a₁₁, a₂₂,…,a_nn образуют главную диагональ определителя, а элементы a_1n, …,a_n1 - побочную.

Определение 2. Рассмотрим прямоугольную матрицу 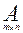. Выделим в этой матрице k различных строк и столбцов, причем 1 ≤ k ≤ min. Элементы выделенных строк и столбцов образуют квадратную матрицу порядка k.

Определитель выделенной квадратной матрицы называется минором k-го порядка заданной матрицы А.

Определение 3. Если в выделенную квадратную матрицу порядка k включены строки и столбцы заданной матрицы, имеющие одинаковые номера, то соответствующий минор k-го порядка называется главным.

Определение 4. В квадратной матрице n-го порядка вычеркнем все элементы i-ой строки и j-го столбца. Оставшиеся элементы образуют квадратную матрицу (n-1)-го порядка. Ее определитель представляет собой минор (n-1)-го порядка. Он называется минором, соответствующим элементу а_ij и обозначается М_ij.

Определение 5. Алгебраическим дополнением элемента a_ij kвадратной матрицы порядка n называется число, определяемое по формуле А_ij = (-1)^I+jМ_ij.

Определители квадратной матрицы наиболее рационально вычислять на основе теоремы Лапласа и свойств определителей.

Теорема Лапласа. (Лаплас Пьер Симон (1749 – 1827г.г.), фр. астроном, математик, физик) Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

В частности, в случае определителя третьего порядка

Δ =

формула разложения его по элементам первой строки будет иметь вид

Δ = а₁₁А₁₁ + а₁₂А₁₂ + а₁₃А₁₃ =

= а₁₁(-1)¹⁺¹М₁₁ + а₁₂(-1)¹⁺²М₁₂ + а₁₃(-1)¹⁺³М₁₃ =

= а₁₁- а₁₂+ а₁₃.

Значение теоремы Лапласа состоит в том, что она позволяет свести вычисление определителей n-го порядка к вычислению более простых определителей (n-1)-го порядка. В частности, с помощью этой теоремы

вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.

Учитывая, что каждый минор (определитель) первого порядка равен единственному элементу соответствующей матрицы, из теоремы Лапласа получаем при n=2:= а₁₁- а₁₂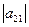= а₁₁а₂₂ - а₁₂а₂₁.

Согласно полученной формуле определитель квадратной матрицы второго порядка равен разности произведений элементов главной и побочной диагоналей.

При n=3 имеем следующую цепочку преобразований:

= а₁₁- а₁₂+ а₁₃=

= а₁₁ (а₂₂а₃₃ – а₃₂а₂₃) - а₁₂(а₂₁а₃₃ – а₃₁а₂₃) + а₁₃(а₂₁а₃₂ – а₃₁а₂₂) =

= а₁₁а₂₂а₃₃ + а₁₂а₂₁а₃₃ + а₁₃а₂₁а₃₂ - а₁₁а₃₂а₂₃ - а₁₂а₃₁а₂₃ - а₁₃а₃₁а₂₂.

Полученный результат легко запомнить, если воспользоваться правилом треугольника (правилом Сарруса) (см. рис. 1.1).

Но в этом нет необходимости. Нужно просто знать и уметь практически применять теорему Лапласа в каждом конкретном случае.

Пример 1.Вычислить определитель

Δ =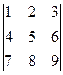

Решение. Используем теорему Лапласа. Для этого разложим определитель Δ по элементам первой строки. Δ = 1х- 2х+ 3х=

= (45-48)-2(36-42)+3(32-35) = -3+12-9 = 0.

Итак, с помощью теоремы Лапласа можно вычислить определитель квадратной матрицы любого порядка. Однако, для матриц 4-го и более высоких порядков расчеты становятся весьма громоздкими. Во многих случаях объем вычислений можно сократить, воспользовавшись свойствами определителей.

Основные свойства определителей

1.Вычисление определителя можно производить с помощью теоремы Лапласа путем разложения по элементам любой строки или любого столбца. Часто случается, что ряд элементов определителя равны нулю. В этом случае разложение производится по элементам той строки (столбца), где имеется наибольшее количество нулевых элементов.

Пример 2. Вычислить определитель Δ = .

Решение. В третьем столбце данного определителя имеется три равных нулю элемента. Поэтому воспользуемся разложением определителя по элементам этого столбца и запишем:

Δ = 3х(-1)¹⁺³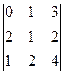

Разлагая далее полученный определитель третьего порядка по элементам первого столбца, находим

Δ = 3х((-2)+ 1) =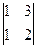

= 3((-2)(4-6) + (2-3)) = 3(4-1) = 3х3 = 9.

2. Определитель квадратной матрицы не меняется при ее транспонировании, т.е. det A = det A^T.

3. Если поменять местами какие – либо две строки (столбца), то определитель изменит знак на противоположный.

4. Если все элементы какого-либо столбца (строки) умножить на одно и то же число λ, то определитель умножится на это же число λ.

Следствие 1. Пусть λ=0. Тогда получается, что определитель, все элементы какого-либо столбца (строки) которого равны нулю, также равен нулю.

Следствие 2. Если все элементы определителя умножить на одно и то же число λ, то определитель изменится в λⁿ раз.

5. Определитель, у которого все элементы двух и более строк (столбцов) соответственно пропорциональны (в частности, равны) равен нулю.

6. Определитель не меняет своего значения от прибавления к элементам какой-либо строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.

Эти свойства легко доказать непосредственным вычислением на примере определителей второго или третьего порядков. Применение указанных свойств позволяет упростить вычисление определителей.

Пример 3. Вычислить определитель Δ =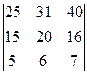

Решение. Непосредственное применение теоремы Лапласа приводит к операциям со сравнительно большими числами. Что усложняет расчеты. Для их упрощения преобразуем заданный определитель. Прибавим к элементам первой строки соответствующие элементы третьей, умноженные на (-5), а к элементам второй – элементы также третьей, умноженные на (-3).

В итоге получим определитель

Δ = =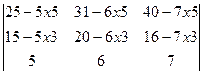

Раскладывая далее Δ по элементам первого столбца, находим

Δ =5(-5-10) = -75.

1.4. Обратная матрица.

Определение. Матрица А^-1 обратная матрица по отношению к квадратной матрице А, если А^-1xА = А x А^-1 = E.

А^-1 существует при условии, что detA ≠0 (такая матрица называется невырожденной).

Например, обратной по отношению к невырожденной матрице А = является матрица А^-1 = .

Действительно, в данном случае имеем:

АxА^-1 = x= = ,

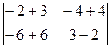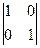также АxА^-1 = x= .

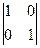Матрица, обратная единичной, также является единичной матрицей. Очевидно, что det(AxB) = detAx detB, detA^-1 = 1/detA.

Приведем (без вывода) правило (алгоритм) вычисления обратной матрицы A^-1:

1) находим detА и проверяем условие detА ≠ 0;

2) находим А^Т;

3) находим А^Т_ij = A_ji (i = 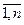; j = 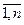) и составляем из них присоединенную матрицу /= А^Т_ij = A_ji (i,j = );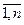

4) вычисляем обратную матрицу по формуле А^-1 = (1/ detА) ;

5)проверяем правильность вычисления обратной матрицы А^-1, исходя из определения: А^-1А = А А^-1 = Е.

Пример. Найти матрицу А^-1, если А =

Решение.

1. Находим detА = = = 14 ≠ 0.

2. А^Т = ;

3. А^Т₁₁ = 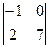= -7, А^Т₁₂ = - 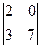= -14, А^Т₁₃ = = 7, А^Т₂₁ = = 6,

А^Т₂₂ = 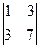= -2, А^Т₂₃ = = -2, А^Т₃₁ = = 3, А^Т₃₂ = = 6,

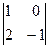А^Т₃₃ = = -1, = .

4. А^-1 = 1/14 х = .

5. Проверяем условие АА^-1 =Е.

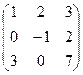х = = Е.

Нетрудно убедиться, что А^-1А=Е.

Свойства невырожденных матриц.

1. 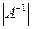= 1/; 2. (А^-1)^-1 = А;

3. (А^m)^-1 = (А^-1)^m; 4. (АВ)^-1 = В^-1А^-1.

1.5. Ранг матрицы.

Всякая матрица, помимо своего порядка m x n характеризуется дополнительным показателем, устанавливающим ее размерность.

Таким показателем является ранг матрицы (от фр., нем..англ.-ранг, размер, порядок).

Определение 1. Рангом матрицы называется максимальный порядок отличных от нуля миноров этой матрицы. При этом отличный от нуля минор наивысшего порядка называется базисным.

Из определения следует, что рангом обладает всякая матрица.

Очевидно:

1) для всякой матрицы А размера m x n ранг r(A) ≤ min(m;n);

2) матрица имеет ранг r, если по крайней мере один из ее миноров порядка r отличен от нуля, а все миноры порядка (r +1) равны нулю;

3) r(А)=0, если А – нулевая матрица.

Пример 1. Найти ранг матрицы A = .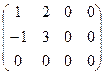

Решение. r(А)=2, так как есть минор второго порядка 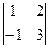= 5 ≠ 0, а все миноры третьего порядка равны нулю. (Убедитесь в этом самостоятельно).

При вычислении ранга матрицы существует два основных способа. Первый связан с вычислением миноров, а второй – с ее элементарными преобразованиями.

К элементарным преобразованиям матрицы относятся, в частности, следующие преобразования:

1) перестановка любых ее строк или столбцов;

2) умножение элементов некоторой строки (или столбца) на число α ≠ 0;

3) прибавление к элементам строки (столбца) элементов другой строки (столбца), умноженных на число α;

4) вычеркивание строки (столбца), все элементы которой равны нулю.

Определение 2. Матрицы А и В называются эквивалентными, если

r(А) = r(B).

Ранг матрицы не изменится от элементарных преобразований. Другими словами, в результате элементарных преобразований исходная матрица преобразуется в эквивалентную матрицу.

При вычислении ранга матрицы первым способом пытаются найти минор второго порядка, отличный от нуля. Если такой минор найден, то далее следует вычислять не все миноры третьего порядка, а только те, которые окаймляют

отличный от нуля минор второго порядка (минор (k + 1)-го порядка называется окаймляющим для минора k-го порядка, если минор k-го порядка сам является минором упомянутого минора (k+1)-го порядка).

Так поступают до тех пор, пока не установят, что все окаймляющие миноры некоторого (r+1)-го порядка равны нулю, а минор r-го порядка отличен от нуля. Тогда r(А)=r.

Пример 2. Вычислить ранг матрицы A = 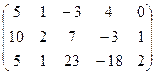методом окаймления миноров.

Решение. 1. Находим минор второго порядка M = = 7 + 6 = 13 ≠ 0.

2.Вычисляем окаймляющие его миноры третьего порядка.

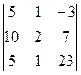= 0, = 0, 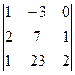= 0 (убедитесь в этом самостоятельно).

Итак, все окаймляющие миноры третьего порядка равны нулю. Следовательно, r(А)=2.

Матричное исчисление представляет собой аппарат решения большого числа теоретических и прикладных проблем. Наряду с числовыми матрицами часто при этом приходится иметь дело с матрицами, элементы которых представляют собой некоторые функции. Такие матрицы называются функциональными.

Дата добавления: 2014-01-05