Элементы двоичной арифметики. Кодирование и обработка чисел в ЭВМ

Двоичная арифметика. Правило сложения двух чисел в двоичной системе счисления:

1) сложение чисел производится поразрядно, начиная с младшего разряда, с использованием таблицы сложения для двоичной системы счисления (табл. 2.1);

2) при сложении цифр в каждом разряде необходимо добавлять к их сумме единицы переноса из младших разрядов.

Таблица 2.1

Сложение +	1-ое слагаемое	2-ое слагаемое	результат

- единицы переноса из младших разрядов

Пример 6. Сложение двух двоичных чисел 1001,01₂ и 1101,11₂.

1 11 1

+ 1001, 01₂

1101, 11₂

1 0111, 00₂

Пример 7. Вычитание двух двоичных чисел 1001,01₂ и 1101,11₂.

1 1 1

1 1 1

- 1 1 0 1, 0 1₂

1 0 0 1, 1 1₂

0 0 1 1, 1 0₂

Для умножения чисел в позиционной системе счисления с любым основанием следует умножить множимое на каждый разряд множителя и просуммировать частные произведения, сдвинутые друг относительно друга на один разряд. Таблица умножения для двоичной системы счисления приведена в табл. 2.2.

Таблица 2.2

Умножение X	множимое	множитель	результат

Пример 8. Умножение двух двоичных чисел 1001₂ и 1101₂.

x 1001₂

1101₂

+

1001

1001

1110101₂

Кодирование и обработка чисел в ЭВМ. Для алгебраического представления чисел, т.е. для представления чисел с учетом их знака, в вычислительных машинах используются специальные коды:

· прямой код числа;

· обратный код;

· дополнительный код.

При этом два последних кода позволяют заменить неудобную для компьютера операцию вычитания на операцию сложения с отрицательным числом. Дополнительный код обеспечивает более быстрое выполнение операций, поэтому в компьютере чаще всего применяется именно он.

Прямой код числа A (обозначим A_пр).

Пусть A = a₁ a₂ а₃..., а_т, тогда:

при A > 0, A_пp = 0, a₁ a₂ а₃..., а_т;

при A<0, A_пp = 1, a₁ a₂ а₃..., а_т;

при A = 0 имеет место неоднозначность A_пр = 0, 0000... = 1, 0000....

Арифметические операции с двоичными числами в прямом коде. Если при сложении в ЭВМ оба слагаемых имеют одинаковый знак, то операция сложения выполняется обычным путем. Если при сложении слагаемые имеют разные знаки, то сначала необходимо выявить большее по абсолютной величине число, из него произвести вычитание меньшего по абсолютной величине числа и разности присвоить знак большего числа.

Выполнение операций умножения и деления в прямом коде выполняется обычным образом, но знак результата определяется по совпадению или несовпадению знаков участвовавших в операции чисел.

Операцию вычитания в этом коде нельзя заменить операцией сложения с отрицательным числом, поэтому возникают сложности, связанные с займом значений из старших разрядов уменьшаемого числа. В связи с этим прямой код в ЭВМ почти не применяется.

Основная идея замены вычитания чисел их сложением заключается в том, что вычитание положительного числа сводится к сложению со специальным кодом отрицательного числа. Для этого область отрицательных чисел переносится в область положительных чисел. Другими словами, в операции участвуют не сами числа, а их изображения.

Обратный код числа A, обозначим A_oбp.

Пусть A = a₁ a₂ а₃..., а_т и 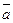обозначает инверсию а, т. е. если а = 1, то 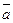= 0, и наоборот. Тогда:

при A > 0, A_oбp = 0, a₁ a₂ а₃..., а_т;

при A< 0, A_обр = 1, ;

при A = 0 имеет место неоднозначность A_обр = 0, 00...0 = 1, 11…1.

Правило. Для того чтобы получить обратный код отрицательного числа, необходимо все цифры этого числа инвертировать, т. е. в знаковом разряде поставить 1, во всех значащих разрядах нули заменить единицами, а единицы нулями.

Это же правило справедливо и при переводе отрицательных чисел из обратного кода в прямой.

Например,

для А = 1001 А _oбp = 0, 1011;

для A = -1010 A_oбp = 1, 0101;

для А_обр = 1, 00110 А = - 11001.

Важно заметить, что в обратном коде отрицательного числа нули, записанные в конце числа (после запятой) и в начале числа (после единицы, отделенной точкой), отбрасывать нельзя!

Сформулируем правило сложения чисел в обратном коде.

Правило. Для того чтобы при сложении обратных кодов двух чисел получить обратный код суммы, необходимо сложить обратные коды слагаемых по правилам сложения двоичных чисел, рассматривая при этом знаковые разряды как обычные цифровые. Если появляется единица переноса из знакового разряда, то ее следует циклически перенести в младший разряд и просуммировать с ранее полученным результатом.

Например, сложить два числа А₁ = + 10100₂ (20₁₀) и А₂ = - 01011₂
(-11₁₀) в обратном коде.

+

А_1обр = 0, 10100

А_2обр = 1, 10100

10, 01000

1

Результат 0, 01001₂ (9₁₀).

Т.к. в знаковом разряде стоит 0, то делаем вывод, что полученное число положительное и его обратный код совпадает с прямым кодом.

Если в результате суммирования в знаковом разряде оказалась 1, то результат – отрицательное число и для получения истинного значения результата требуется перевести его в прямой код, инвертируя цифры всех разрядов, кроме знакового.

Дополнительный код числа A, обозначим A _доп.

Пусть, как и выше, A = a₁ a₂ а₃... а_т и 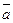обозначает величину, обратную а (инверсию а), т.е. если а= 1, то 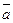= 0, и наоборот. Тогда:

при А > 0, A_доп = 0, a₁ a₂ а₃..., а_т;

при А < 0, А_дon = 1, + 0,000... 1.

Правило. Для того чтобы получить дополнительный код отрицательного числа, необходимо все его цифры инвертировать (в знаковом разряде поставить единицу, во всех значащих разрядах нули заменить единицами, а единицы - нулями) и затем к младшему разряду прибавить единицу. В случае возникновения переноса из первого после запятой разряда в знаковый разряд к числу следует прибавить единицу в младший разряд.

Например,

для А= 1011₂, А _доn = 0, 1011₂;

для А = - 1100₂, А _доп = 1, 0100₂;

для А = -0000₂, А _доп = 10, 0000₂ = 0,0000₂ (1 исчезает). Неоднозначности в изображении нуля нет.

Эмпирическое правило: для получения дополнительного кода отрицательного числа необходимо все символы этого числа инвертировать, кроме последней (младшей) единицы и тех нулей, которые за ней следуют.

Для образования прямого кода отрицательного числа из дополнительного нужно вычесть из дополнительного кода единицу младшего разряда (получить обратный код) и заменить единицы нулями, а нули единицами (получить прямой код).

Например, перевести число А из дополнительного кода в прямой.

А _доп = 1, 11011.101₂ А _обр = 1, 11011.100₂

А _пр = 1, 00100.011₂

Рассмотренный метод перевода неудобен тем, что содержит операцию вычитания. В ЭВМ прямой код отрицательного числа получают путем образования дополнительного кода от дополнительного, т.е. образуется обратный код и к нему прибавляется единица младшего разряда.

Ноль в дополнительном коде имеет единственное представление: [0] _доп = 0, 00...00.

Сформулируем правило сложения чисел в дополнительном коде.

Правило. Для того чтобы при сложении дополнительных кодов двух чисел получить дополнительный код суммы, необходимо сложить дополнительные коды слагаемых по правилам сложения двоичных чисел, рассматривая знаковые разряды как обычные цифровые. При возникновении единицы переноса из знакового разряда ее следует опустить (не учитывать).

Например, сложить два числа А = + 1101.01₂ (13,25₁₀) и
В = -110.011₂ (-6,375₁₀) в дополнительном коде.

А _доп = 0, 1101.01₂ B _доп = 1, 1001.101₂ А _доп = 0, 1101.010

+

B _доп = 1, 1001.101

1 0, 0110.111

1опускается

Ответ: А _доп + B _доп = 0, 0110.111₂ (6,875₁₀)

Сложить два числа А = -1001,1₂ и В=- 11,1001₂ вдополнительном коде.

А _доп = 1, 0110.1000

+

B _доп = 1, 1100.0111

1 1, 0010.1111

1опускается

Ответ: А _доп + B _доп = 1, 0010.1111₂

При сложении может возникнуть ситуация, когда старшие разряды результата операции не помещаются в отведенной для него области памяти. Такая ситуация называется переполнением разрядной сетки формата числа.

Например, сложить два числа A = +17563₁₀ и В = +19157₁₀ в дополнительном коде.

А _доп = 0, 100 0100 1001 1011₂ B _доп= 0, 100 1010 1101 0101₂.

+

0, 100 0100 1001 1011

0, 100 1010 1101 0101

1, 000 1111 0111 0000₂

Т.е. при сложении двух положительных чисел получен отрицательный результат - переполнение.

Или, например, требуется сложить два числа A = -17563₁₀ и
В = -19157₁₀ в дополнительном коде.

А _доп = 1, 011 1011 0110 0101₂ B_доп= 1, 011 0101 0010 1011₂.

+

1, 011 1011 0110 0101

1, 011 0101 0010 1011

1 0, 111 0000 1001 0000₂

Т.е. при сложении двух отрицательных чисел получен положительный результат - переполнение.

Для обнаружения переполнения и оповещения о возникшей ошибке в компьютере используются специальные средства. В процессоре ЭВМ содержаться два индикатора - индикатор переноса и индикатор переполнения. Каждый индикатор содержит 1 бит информации и может иметь значение, равное 1 (индикатор установлен) или 0 (индикатор сброшен). Индикатор переноса указывает перенос из знакового бита, а индикатор переполнения - на перенос в знаковый бит. Таким образом, после завершения операции, в которой происходит перенос в старший бит, процессор устанавливает индикатор переполнения. Если такого нет, то индикатор переполнения сбрасывается. Индикатор переноса обрабатывается аналогичным образом.

После выполнения операции процессором ЭВМ сигнализирует о состоянии индикаторов, и их можно проверить. Если состояние индикаторов указывает на неправильный результат, то необходимо предпринять меры, исправляющие эту ситуацию, т.е. пользователю ЭВМ предоставляется возможность контролировать правильность выполнения арифметических операций.

§ 2.3. Кодирование текстовой,

Дата добавления: 2014-01-05