Связь между дирекционными углами предыдущей и последующей линий

Обратная геодезическая задача

Прямая геодезическая задача

Обратная геодезическая задача

Прямая геодезическая задача

Прямая и обратная геодезические задачи

В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояние S_AB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол α_AB или румб r_AB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.

Рис. 23. Прямая геодезическая задача

Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом.

Дано: Точка А(X_A, Y_A), S_AB и α_AB.

Найти: точку В(X_B, Y_B).

Непосредственно из рисунка имеем:

ΔX = X_B – X_A;

ΔY = Y_B – Y_A.

Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:

ΔX = S_AB · cos α_AB;

ΔY = S_AB · sin α_AB.

Так как в этих формулах S_AB всегда число положительное, то знаки приращений координат ΔX и ΔY зависят от знаков cos α_AB и sin α_AB. Для различных значений углов знаки ΔX и ΔY представлены в табл.1.

Таблица 1.

Знаки приращений координат ΔX и ΔY

Приращения координат	Четверть окружности в которую направлена линия
I (СВ)	II (ЮВ)	III (ЮЗ)	IV (СЗ)
ΔX	+	–	–	+
ΔY	+	+	–	–

При помощи румба приращения координат вычисляют по формулам:

ΔX = S_AB · cos r_AB;

ΔY = S_AB · sin r_AB.

Знаки приращениям дают в зависимости от названия румба.

Вычислив приращения координат, находим искомые координаты другой точки:

X_B = X_A + ΔX;

Y_B = Y_A+ ΔY.

Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения.

Обратная геодезическая задача заключается в том, что при известных координатах точек А (X_A, Y_A) и В (X_B, Y_B) необходимо найти длину S_AB и направление линии АВ: румб r_AB и дирекционный угол α_AB (рис.24).

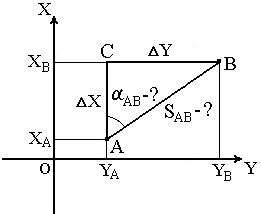
Рис. 24. Обратная геодезическая задача

Даннная задача решается следующим образом.

Сначала находим приращения координат:

ΔX = X_B – X_A;

ΔY = Y_B – Y_A.

Величину угла r_AB определем из отношения

ΔY	= tg rAB
ΔX

.

По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим α_AB.

Для контроля расстояние S_AB дважды вычисляют по формулам:

SAB=	ΔX	=	ΔY	= ΔX · sec αAB = ΔY · cosec αAB
cos αAB	sin αAB

SAB=	ΔX	=	ΔY	= ΔX · sec rAB = ΔY · cosec rAB
cos rAB	sin rAB

Расстояние S_AB можно определить также по формуле

.

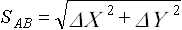На рис. 25 представлена схема определения дирекционных углов сторон теодолитного хода AB. Известен дирекционный угол исходной стороны α₀ и измерены геодезическим прибором теодолитом углы β₁, β₂, β₃, лежащие справа по ходу от А к В.

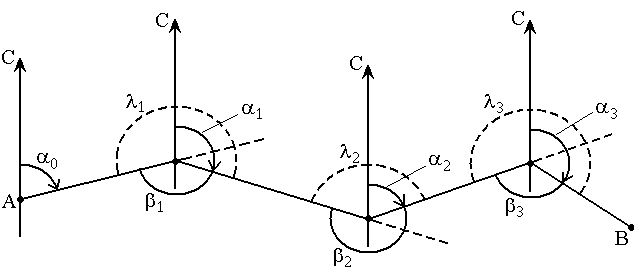
Рис. 25. Схема определения дирекционных углов сторон теодолитного хода

Найдём дирекционные углы α₁, α₂, α₃ остальных сторон хода.

На основании зависимости между прямыми и обратными дирекционными углами можем написать:

α₁ + β₁ = α₀ + 180° из данного выражения следует, что α₁ = α₀ + 180° – β₁ (1).

Аналогично вычисляются дирекционные углы последующих сторон теодолитного хода:

α₂ + β₂ = α₁ + 180° → α₂ = α₁ + 180° – β₂ (2)

α₃ + β₃ = α₂ + 180° → α₃ = α₂ + 180° – β₃ (3)

...............................................................................

α_n + β_n = α_n-1 + 180° → α_n = α_n-1 + 180° – β_n (n)

То есть, дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180° и минус угол, лежащий справа по ходу.

Для получения контрольной формулы в выражение (2) подставим значение α₁, из выражения (1)

α₂ = α₀ + 2 ∙ 180° – (β₁ + β₂).

Если продолжить аналогичные действия для последующих сторон теодолитного хода, то получим

α_n = α₀ + n ∙ 180° – (β₁ + β₂ + β₃ +... + β_n).

или

α_n – α₀ = n ∙ 180° – ∑β.

или

α₀ – α_n = ∑β – n ∙ 180°.

Эта формула может служить контрольной при вычислении дирекционных углов по увязанным углам β.

Если же вместо суммы исправленных углов подставить сумму измеренных углов ∑β, то та же формула позволит определить невязку f_β измеренных углов теодолитного хода, если дирекционные углы α₀ и α_n начальной и конечной сторон хода известны

f_β = ∑β – n ∙ 180° – (α₀ – α_n).

Иногда дирекционные углы вычисляют по углам, лежащим слева по ходу от А до В (λ₁, λ₂, …, λ_n).

β₁ = 360° – λ₁

β₂ = 360° – λ₂

........................

β_n = 360° – λ_n

Подставим эти значения в выражения (1), (2),..., (n) получим

α₁ = α₀ – 180° + λ₁

α₂ = α₁ – 180° + λ₂

.................................

α_n = α_n-1 – 180° + λ_n.

Для проверки правильности вычисления дирекционных углов по углам λ, лежащим слева по ходу, используют выражения

α_n – α₀ = ∑λ – n ∙ 180°

или

α_n – α₀ = ∑λ + n ∙ 180°.

Тогда невязка f_β определяется по формуле

f_β = ∑λ + n ∙ 180° – (α_n – α₀).

Лекция 3. Геодезическая съемка. Рельеф, его изображение на картах и планах.
Цифровые модели местности

3.1. Геодезическая съемка. План, карта, профиль

3.2. Рельеф. Основные формы рельефа

3.3. Изображение рельефа на планах и картах

3.4. Цифровые модели местности

3.5. Задачи, решаемые на планах и картах

3.6. Вопросы для самоконтроля

Дата добавления: 2014-01-05