Передаточные функции для выходного сигнала

Если в качестве входа АС принять ошибку отработки задающего воздействия 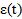, то зависимость выходного сигнала 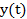от входных воздействи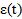й и 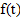при начальных нулевых условиях можно представить дифференциальным уравнением:

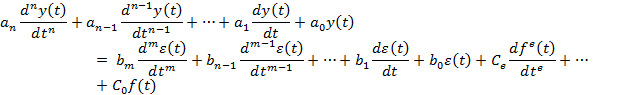(1.27)

Это уравнение определяет динамику процессов регулирования в разомкнутой системе. В операторной системе оно имеет вид

(1.28)

где А(р) – характеристический полином разомкнутой системы;

В(р) – полином управляющего воздействия;

С(р) – полином возмущающего воздействия.

Связь между выходным сигналом разомкнутой системы, управляющим и возмущающим воздействиями можно представить в виде:

(1.29)

т.е. выходной сигнал является суммой реакций АС на управляющее м возмущающее воздействия.

Следовательно, соотношение

, (1.30)

представляет собой передаточную функцию разомкнутой системы по управляющему воздействию, а соотношение

(1.31)

передаточную функцию разомкнутой системы по возмущающему воздействию.

Передаточная функция К_р(р) часто называется передаточной функцией разомкнутой системы. Из схемы (см. рис. 1.9) видно, что при выполнении условия (1.30) справедливо равенство

.

Из соотношения (1.31) следует, что .

Для нахождения передаточных функций замкнутой системы подставим в уравнение (1.28) уравнение замыкания (1.25). В результате подстановки получим

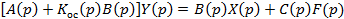
. (1.32)

Обозначим Выражение D(p) называется характеристическим полиномом замкнутой АС, а уравнение

(1.33)

называется характеристическим уравнением замкнутой системы. С учетом выражения (1.30) характеристическое уравнение замкнутой системы можно записать в виде

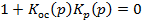
(1.34)

Характеристические полиномы разомкнутой А(р) и замкнутой D(p) систем, а также корни соответствующих характеристических уравнений играют важную роль при исследовании динамических свойств АС.

Из уравнения (1.32) связь между выходным сигналом замкнутой системы, управляющим и возмущающим воздействиями устанавливаются выражением

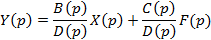
(1.35)

Отсюда следует, что выражение

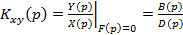(1.36)

Является передаточной функцией замкнутой системы по управляющему воздействию, а выражение

(1.37)

Передаточной функцией замкнутой системы по возмущающему воздействию.

Учитывая соотношения между полиномами D(p), A(p), B(p), C(p), получим из уравнений (1.30), (1.31), (1.35), и (1.36)

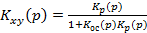(1.38)

. (1.39)

Передаточная функция K_xy(p) часто называется передаточной функцией замкнутой системы и обозначается К_з(р).

Передаточные функции (1.38) и (1.39) легко определить непосредственно по структурной схеме конкретной автоматической системы. При этом передаточная функция разомкнутой системы по возмущению будет зависеть от точки приложения возмущающего воздействия, в то время как точка приложения управляющего воздействия и выход системы считаются заданными вместе со структурной АС.

Полученные формулы легко обобщить на случай произвольного количества управляющих x₁(t)….x_m(t) и возмущающих f₁(t)…..f_e(t) воздействий. Обозначив частные передаточные функции по управляющим воздействиям по принципу суперпозиции получим

(1.40)

В данном случае передаточные функции K_xiY(p) также будут зависеть от точки приложения управляющего сигнала.

Дата добавления: 2014-01-05