Пример 2. Рассмотрим детерминированную систему с непрерывным временем. Такая система описывается дифференциальным уравнением

Пусть дан колебательный механизм

Запишем все силы действующие на объект:

F_ин+ F_тр+ F_{упр пруж}= F(t)

Сила инерции груза равна произведению массы груза на ускорение его движения и направлена в сторону, противоположную направлению ускорения

Cила трения всегда направлена противоположно действующей на тело внешней силе, стремящейся привести это тело в движение Fтр = kN, где k коэффициент трения, N – сила реакции опоры, соответствующая силе давления, производимой телом на поверхность. Если тело находится на горизонтальной поверхности, то N = Fтяж=mg.

Полученная модель системы в переменных «вход-выход» представляет собой дифференциальное уравнение 2 -го порядка.

В общем виде модель системы в переменных «вход-выход» представляет собой дифференциальное уравнение n-го порядка.

Описание системы в переменных состояния (в нормальной форме Коши).

Модель системы в переменных состояния так же имеет вид дифференциальных уравнений, но записывается в специальной форме – как система уравнений первого порядка.

Обычно модель в переменных состояния представляют в векторно-матричной форме.

Смысл модели в переменных состояния (или модели в пространстве состояний) заключается в том, что она сохраняет соотношения между входом с выходом системы, но в тоже время позволяет перейти от одного дифференциального уравнения n - го порядка к системе n дифференциальных уравнений первого порядка.

Преимущество такого представления в том, что:

- кроме двух внешних переменных (входной и выходной), в модели отражаются и все внутренние переменные системы.

- модель в переменных состояния для систем высокого порядка (т.е. система представленных дифференциальным уравнением высокого порядка) позволяет легко решать задачи анализа и синтеза с помощью методов решения системы диф. ур-ий с использованием ЭВМ.

- имея модель в переменных состояния, мы получаем больше информации об объекте управления (о его внутренних переменных); следовательно, процедура проектирования системы управления может быть выполнена более эффективно.

Переменными состояния x(i), i=1, 2, …, n динамической системы называют такие независимые переменные, набор которых, достаточен для полного математического описания состояния системы в динамике.

Полное математическое описание состояния системы в динамике означает, что

(имея) - по заданным значениям х₁₀, х₂₀, …, х_n0 всех переменных состояния в некоторый фиксированный момент времени t=t₀,

(имея) - по заданным значениям воздействий во все последующие моменты t>t₀

(имея) - и по уравнениям системы

можно определить значения всех переменных состояния в любой последующий момент времени t>t₀.

Уравнения звеньев обычно записываются через переменные состояния x(t) в нормальной форме, в виде системы дифференциальных уравнений 1-го порядка, разрешенных относительно первых производных (форма Коши):

ПРИМЕР - 3 - Рассмотрим систему, описываемую дифференциальными уравнениями:

,

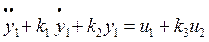где, u₁ и u₂ – входные переменные,

а y₁ и y₂ – выходные переменные.

Зависимость переменных от времени для удобства опущена.

За переменные состояния мы принимаем

- выходы системы

- и их производные (при необходимости).

Перепишем исходную систему уравнений с учетом вновь введенных переменных:

,

,

.

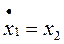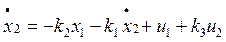Система уравнений дополняется уравнениями для выходных переменных:

,

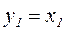Левая часть дифференциальных уравнений относительно x(t) всегда представлена только первыми производными переменных состояния, правая же часть не должна содержать никаких производных.

В уравнениях относительно выхода y(t) всегда так же не должно быть никаких производных.

Мы получили систему из 5 дифференциальных уравнений первого порядка – модель системы в пространстве состояний.

Полученная система уравнений может быть записана в векторно-матричной форме:

,

.

Математические модели детерминированных систем функционирующих в дискретные моменты времени являются различные схемы конечных автоматов.

Конечный автомат функционирует в дискретные моменты времени: t₀, t₁, t₂, …

Dt=t_i+1 - t_i

Если за единицу времени взять Dt, то можно сказать что конечный автомат принимает значения: 0, 1, 2, …

Для конечного автомата множество состояний системы и множества входных и входных воздействий являются конечными.

Z={Z₁, Z₂, … Z_n }

X={X₁, X₂, … X_n}

Y={Y₁, Y₂, … Y_n}

Конечный автомат функционирует следующим образом:

- В момент времени t поступает входное воздействие X(t), которое переводит автомат в новое состояние в соответствии с функцией перехода: Z(t+1)=F(Z(t), X(t))

- При этом выходное воздействие определяется по формуле выхода: Y(t)=F(Z(t), X(t))

Пример задания конечного автомата.

Абстрактный автоматА задается как совокупность:

1. конечного множества X входных сигналов – называемого входным алфавитом;

2. конечного множества Y выходных сигналов – называемого выходным алфавитом;

3. произвольного конечного множества Z состояний автомата;

4. начальное состояние автомата Z(0)=Z₀, в начальный момент времени t=0 автомат всегда находится в своем начальном состоянии Z₀;

5. функция переходов автомата;

6. функция выходов автомата;

7. задание таблиц переходов и выходов и/или построение направленного графа.

Чтобы задать конечный автомат, необходимо описать входной и выходной алфавиты, задать начальное состояние автомата и множество его промежуточных состояний, а так же записать функции его переходов и выходов.

Простейший табличный способ задания конечного автомата основан на использовании таблиц переходов и выходов.

Строки обеих этих таблиц обозначаются входными сигналами автомата, а столбцы – его состояниями. На пересечении строки и столбца таблицы переходов ставится соответствующее значение функции переходов, а в таблице выходов – соответствующее значение функции выходов.

Второй способ задания автоматов основан на использовании направленных графов.

Вершины графа отождествляются с состояниями автомата, а стрелки с выходными сигналами. Если входной сигнал вызывает переход автомата из одного состояния в другое то на графе этому сигналу соответствует стрелка соединяющая соответствующие вершины.

Переход от задания конечного автомата с помощью таблиц к заданию с помощью графа и обратный переход выполняются вполне очевидным образом.

Дата добавления: 2014-01-05