Процесс моделирования

Процесс моделирования включает три элемента:

1) субъект (исследователь),

2) объект исследования,

3) модель, определяющую (отражающую) отношения познающего субъекта и познаваемого объекта.

Первый этап построения модели предполагает наличие некоторых знаний об объекте-оригинале. Познавательные возможности модели обусловливаются тем, что модель отображает (воспроизводит, имитирует) какие-либо существенные черты объекта-оригинала. Вопрос о необходимой и достаточной мере сходства оригинала и модели требует конкретного анализа. Очевидно, модель утрачивает свой смысл как в случае тождества с оригиналом (тогда она перестает быть моделью), так и в случае чрезмерного во всех существенных отношениях отличия от оригинала. Таким образом, изучение одних сторон моделируемого объекта осуществляется ценой отказа от исследования других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько «специализированных» моделей, концентрирующих внимание на определенных сторонах исследуемого объекта или же характеризующих объект с разной степенью детализации.

На втором этапе модель выступает как самостоятельный объект исследования. Одной из форм такого исследования является проведение «модельных» экспериментов, при которых сознательно изменяются условия функционирования модели и систематизируются данные о её «поведении». Конечным результатом этого этапа является множество (совокупность) знаний о модели.

На третьем этапе осуществляется перенос знаний с модели на оригинал — формирование множества знаний. Одновременно происходит переход с «языка» модели на «язык» оригинала. Процесс переноса знаний проводится по определенным правилам. Знания о модели должны быть скорректированы с учетом тех свойств объекта-оригинала, которые не нашли отражения или были изменены при построении модели.

Четвёртый этап — практическая проверка получаемых с помощью моделей знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им.

Моделирование — циклический процесс. Это означает, что за первым четырёхэтапным циклом может последовать второй, третий и т. д. При этом знания об исследуемом объекте расширяются и уточняются, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, обусловленные малым знанием объекта или ошибками в построении модели, можно исправить в последующих циклах.

Сейчас трудно указать область человеческой деятельности, где не применялось бы моделирование. Разработаны, например, модели производства автомобилей, выращивания пшеницы, функционирования отдельных органов человека, жизнедеятельности Азовского моря, последствий атомной войны. В перспективе для каждой системы могут быть созданы свои модели, перед реализацией каждого технического или организационного проекта должно проводиться моделирование.

Математическое моделирование — это процесс построения и изучения математических моделей, заменяющих реальные объекты. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект, построенный на этапе содержательного моделирования.

Никакое определение не может в полном объёме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты.

Определение модели по А.А.Ляпунову: Моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель):

1. находящаяся в некотором объективном соответствии с познаваемым объектом;

2. способная замещать его в определенных отношениях;

3. дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте.

По учебнику Советова и Яковлева: «модель (лат. Modulus — мера) — это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала». «Замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели называется моделированием». «Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи».

По Самарскому и Михайлову, математическая модель — это «„эквивалент“ объекта, отражающий в математической форме важнейшие его свойства — законы, которым он подчиняется, связи, присущие составляющим его частям, и т.д.» Существует в триадах «модель - алгоритм - программа». «Создав триаду „модель-алгоритм-программа“, исследователь получает в руки универсальный, гибкий и недорогой инструмент, который вначале отлаживается, тестируется в пробных вычислительных экспериментах. После того как адекватность (достаточное соответствие) триады исходному объекту установлена, с моделью проводятся разнообразные и подробные „опыты“, дающие все требуемые качественные и количественные свойства и характеристики объекта».

По монографии Мышкиса: «Перейдем к общему определению. Пусть мы собираемся исследовать некоторую совокупность 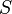свойств реального объекта 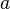с помощью математики (здесь термин объект понимается в наиболее широком смысле: объектом может служить не только то, что обычно именуется этим словом, но и любая ситуация, явление, процесс и т.д.). Для этого мы выбираем (как говорят, строим) „математический объект“ — систему уравнений, или арифметических соотношений, или геометрических фигур, или комбинацию того и другого и т.д.,— исследование которого средствами математики и должно ответить на поставленные вопросы о свойствах 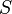. В этих условиях называется математической моделью объекта 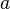относительно совокупности 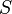его свойств».

По Севостьянову А. Г.: «Математической моделью называется совокупность математических соотношений, уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому процессу, объекту или системе».

Несколько менее общее определение математической модели, основанное на идеализации «вход — выход — состояние», заимствованной из теории автоматов, даёт Wiktionary: «Абстрактное математическое представление процесса, устройства или теоретической идеи; оно использует набор переменных, чтобы представлять входы, выходы и внутренние состояния, а также множества уравнений и неравенств для описания их взаимодействия».

Наконец, наиболее лаконичное определение математической модели: «Уравнение, выражающее идею».

Классификация моделей

используемые математические средства Формальная классификация моделей

Формальная классификация моделей основывается на классификации. Часто строится в форме дихотомий. Например, один из популярных наборов дихотомий:

v Линейные или нелинейные модели;

v Сосредоточенные или распределённые системы;

v Детерминированные или стохастические;

v Статические или динамические;

v Дискретные или непрерывные и т.д.

Каждая построенная модель является линейной или нелинейной, детерминированной или стохастической, … Естественно, что возможны и смешанные типы. способ представления объекта

Классификация по способу представления объекта

Наряду с формальной классификацией, модели различаются по способу представления объекта:

v Структурные модели – представляют объект как систему со своим устройством и механизмом функционирования.

v Функциональные модели не используют таких представлений и отражают только внешне воспринимаемое поведение (функционирование) объекта. В их предельном выражении они называются также моделями «чёрного ящика».

Возможны также комбинированные типы моделей, которые иногда называют моделями «серого ящика».

Дата добавления: 2014-01-05