Восьмеричная и шестнацатиричная системы счисления

Двоичная система, в которой работает ЭВМ, не удобна для восприятия человеком. Большое количество разрядов двоичного числа по сравнению с соответствующим десятичным, однообразное чередование единиц и нулей является источником ошибок и затрудняет чтение двоичного числа. Поэтому для удобства записи двоичных чисел необходима такая система счисления, которая, с одной стороны, сохраняла бы свойства двоичной, а с другой - в написании была бы близка к десятичной. Такими свойствами обладают системы счисления с основанием 2ⁿ, например, 2³ - восьмеричная и 2⁴ - шестнадцатиричная системы счисления.

Эти системы удобны тем, что в них обеспечивается чрезвычайно легкий (в уме) перевод из двоичной системы и в тоже время сохраняется привычный для человека вид числа.

Запишем числа в восьмеричной и шестнадцатиричной системах счисления и их представление в двоичной системе.

Таблица 1

Восьмеричный Шестнадцатиричный Двоичное

символ символ представление

0 0 0

1 1 1

2 2 10

3 3 11

4 4 100

5 5 101

6 6 110

7 7 111

------------- ----------

8 1000

9 1001

A 1010

B 1011

C 1100

D 1101

E 1110

F 1111

Как видим для представления в двоичной системе счисления любого символа восьмеричной системы достаточно трех (триады) двоичных символов. шестнадцатиричного - четырех (тетрады) двоичных символов. Поэтому процедура перевода состоит в следующем:

1) Разбить исходное двоичное число на группы, состоящие из трех двоичных символов (триады) при переводе в восьмеричную систему, и на группы из четырех двоичных символов (тетрады) при переводе в шестнадцатиричную систему, осуществляя разбивку вправо и влево от запятой. Если крайние левые или правые триады (тетрады) окажутся неполными, то они дописываются справа и слева фиктивными нулями.

2) Каждой триаде (тетраде) ставятся в соответствие восьмеричный (шестнадцатиричный) символ.

Пример 1. Записать в восьмеричной системе двоичное число: 1101011,00111011₂

Разбиваем число на триады, начиная от запятой. Далее пользуясь таблицей получаем.

Ответ: 1101011,00111011₂ = 153,166₈

Пример 2. Записать в двоичной системе восьмеричное число: 135, 27₈

Каждую цифру числа представляем в виде двоичной триады в соответствии с таблицей получаем.

Ответ: 135, 27₈ = 1011101,010111₂

Пример 3. Записать в шеснадцатиричной системе двоичное число: 1101011,00111011₂

Разбиваем число на тетрады от запятой влево и вправо. Затем пользуясь таблицей, записываем каждую тетраду числом в шестнадцатиричной системе.

Ответ: 1101011,00111011₂ = 6B,3B ₁₆

Пример 4. Записать в двоичной системе шеснадцатиричное число: 1A,CC₁₆

Пользуясь таблицей запишем каждый шестнацатиричный символ тетрадой двоичных.

Ответ: 1A,CC₁₆ = 11010, 110011₂

Представление данных в ЭВМ. При вводе информации в ЭВМ каждый символ (буквы, символы, цифры, знаки пунктуации и т.п.) кодируются определенной последовательностью двоичных цифр в соответствии с существующими таблицами кодировки: ДКОИ, КОИ-8, ASCII.

Таблица разбита на 16 строк и 16 столбцов, имеющих двоичные номера от 0000 до 1111 или шестнадцатиричные от 0 до F. на пересечении столбцов и строк записаны символы. Код символа составляется из номера столбца, к которому приписывается номер строки.

Таблица 2

Таблица двоичного кода обработки информации (ASCII)

первая шестнадцатиричная цифра кода

0 1 2 3 4 5 6 7 8 9 A B C D E F

P

A

Q

B

R

C

S

D

T

E

U

F

V

G

W

(

H

X

)

I

Y

*

:

J

Z

+

;

K

[

L

\

M

]

N

O

Например, буква F, находящаяся в таблице ASCII в столбьце 0100₂ (4₁₆) на строке 0110₂ (6₁₆), в машине представляется кодом 0100 0110₂, включающим восемь двоичных разрядов или бит.

Бит - это количество информации, которое можно записать в одном двоичном разряде. Двоичный разряд может принимать значение либо 1, либо 0. Комбинация из 8 бит называется байтом. Таким образом, в ЭВМ каждый символ входной информации представляется одним байтом.

Объем памяти обычно выражается в килобайтах. 1 Килобайт = 1024 байтам и обозначается буквой К. Например, компьютер с объемом памяти в 64К может хранить 64*1024=65536 символов.

Поскольку объем памяти ПК постоянно возрастает, была введена еще одна единица измерения памяти “мегабайт”, которая означает миллион байт. Например, в 10 мегабайтах может храниться приблизительно 10 млн. символов.

Формы представления числовой информации в ЭВМ. Различают две основные формы представления чисел: с фиксированной и плавающей точкой. Запись числа в форме с фиксированной точкой характеризуется тем, что число представляется как упорядоченная последовательность коэффициентов формулы (1). Каждому коэффициенту ставится в соответствие один разряд, а точка может фиксироваться между какими-то определенными разрядами, причем для точки никакого разряда не требуется.

qⁿ q^n-1 q¹ q⁰

0 1... n-1 n

Если точка фиксируется непосредственно правее младшего разряда, то в такой разрядной сетке могут быть представлены только целые числа.

Если точка фиксируется непосредственно левее старшего разряда, то в данной разрядной сетке могут быть представлены только правильные дроби.

В памяти ЭВМ число с фиксированной точкой представляет собой целое число со знаком, у которого условная точка согласно принятому соглашению находится справа от самой младшей цифры числа.

Нулевой разряд отводится под знак числа (0 - положительное, 1 - отрицательное).

знак целая часть числа

0 1 15/31/63

Число в форме с плавающей точкой имеет вид:

A = 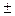m q

где m - мантисса числа; q - основание системы счисления; p - порядок числа в системе с основанием q.

С технической точки зрения более удобно иметь в ЭВМ не порядок, а характеристику числа P*, значение которой связано с порядком числа соотношением, P* = 64 + P. В результате порядок чисел с плавающей точкой в ЭВМ оказывается представленным с избытком 64.

знак характеристика(P*) мантисса(m)

0/1 7 8 31/63

Дата добавления: 2014-01-05