
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства метода резолюций
|
|
|
|
Несмотря на известные недостатки, заключающиеся главным образом в возможности неограниченного порождения резольвент и в отсутствии, тем самым, гарантий быстрого поиска решения, метод резолюций является одном из самых мощных инструментов в решении задач логического вывода. Он обладает двумя существенными достоинствами: он логичен, т.к. резольвенты являются логическими следствиями предложений-родителей, и он обладает полнотой, т.к. при использовании в процессе вывода результат получается за счет применения только одного и того же правила. Представляет интерес свойство завершаемости метода резолюций: если множество {H} невыполнимо, то пустой дизъюнкт может быть найден посредством резолюций. Это и понятно: пустой дизъюнкт есть резольвента множества {H} и, будучи невыполнимым, не может быть следствием выполнимого множества. По этому поводу даже есть лемма:
если множество {H} невыполнимо и содержит резольвенты своих элементов, то оно обязательно содержит пустой дизъюнкт.
Метод резолюций применяется не только в рамках исчисления высказываний и исчисления предикатов (см. последующие главы), к нему нередко сводится процедура вывода в некоторых других моделях представления знаний (продукционные ПЗ, семантические сети, фреймы). Широко известный язык программирования ПРОЛОГ специально создан для реализации процедур, основанных на методе резолюций. Что же касается указанных недостатков, то в значительной степени они уменьшаются или даже исключаются путем применения специальной стратегии целенаправленного поиска резольвент. Ниже мы коснемся этого подробнее.
Основное назначение метода резолюций - порождение логических следствий из системы гипотез {H} (причем эта система должна быть представлена в конъюнктивной нормальной форме). Это может быть порождение с целью общего обзора следствий, или же это будет поиск пустого дизъюнкта при реализации принципа дедукции - меняется только цель. Резольвента есть логическое следствие своих родителей. Обратного утверждать нельзя!
Рассмотрим показательный пример. Обратимся все к тому же свойству транзитивности импликации: если (a ® b) и (b ® c), то (a ® c). Иначе: [(a ® b)(b ® c)] 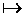
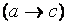 . Гипотезы в нашем примере: H1: (a ® b) и H2: (b ® c), формула B: (a ® c). Согласно принципу дедукции, условие выполняется, если показано, что (H1, H2,
. Гипотезы в нашем примере: H1: (a ® b) и H2: (b ® c), формула B: (a ® c). Согласно принципу дедукции, условие выполняется, если показано, что (H1, H2, 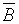 )
) 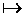 Л. Переходя к КНФ, получаем выражение [(
Л. Переходя к КНФ, получаем выражение [(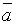 + b)(
+ b)(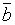 + c)(
+ c)(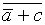 )]
)]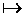 Л. Задача, таким образом, сводится к знакомой формулировке: доказать невыполнимость множества дизъюнктов: (
Л. Задача, таким образом, сводится к знакомой формулировке: доказать невыполнимость множества дизъюнктов: (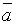 + b), (
+ b), (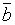 + c), a,
+ c), a, 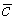 . (т.к
. (т.к 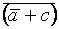 = a Ù
= a Ù 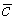 - это два однолитерных дизъюнкта a и
- это два однолитерных дизъюнкта a и 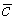 ).
).
Дизъюнкты:
1. 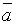 + b,
2. + b,
2. 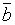 + c,
3. a,
4. + c,
3. a,
4. 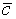
| Резольвенты: 5. b (1,3), 6. c (2,5), 7. Л (4,6). |
Транзитивность доказана, и "по логике" это легко понять: если из a следует b, а из b следует c, то очевидно, что из a следует c. Интересно, будет ли логическим следствием из указанных дизъюнктов какой-либо другой из них? Например, `b + c. То есть требуется доказать:
[(a ® b)(a ® c)] 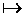 (b ® c).
(b ® c).
Переходя к КНФ, имеем дизъюнкты: (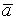 + b), (
+ b), (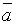 + c),
+ c), 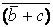
 или иначе (
или иначе (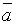 + b), (
+ b), (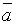 + c), b,
+ c), b, 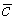 .
. 
Итак, дизъюнкты: Резольвенты:
1. 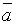 + b, 5.
+ b, 5. 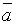 . (2,4)
. (2,4)
2. 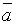 + c, Других резольвент нет.
+ c, Других резольвент нет.
3. b, Импликация (b ® c) не является
4. 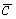 . логическим следствием.
. логическим следствием.
Оно и правда: из того, что b и c следуют из а вовсе не следует, что c следует из b.
Из примера выводим:
если резольвента Bi есть логическое следствие из {H}, то совсем не обязательно, чтобы хотя бы для одной гипотезы Hk выполнялось условие
(H1, H2,.. Hn, Bi) 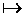 Hk.
Hk.
Разберем еще несколько примеров.
Пример 1. Пусть даны посылки p и p ® q. Определить все возможные следствия из этой пары. Систематический обзор логических следствий удобно осуществлять путем обращения к совершенной конъюнктивной нормальной форме (СКНФ). Напомним, что особенность СКНФ заключается в том, что все ее конъюнктивные члены содержат все переменные данной формулы и, следовательно, имеют одинаковое число литер. Если какой-либо член СКНФ содержит меньшее число переменных, то недостающие переменные вводятся прибавлением формулы типа a Ù 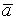 , которая равна 0 и на дизъюнкцию не влияет. Затем эту конъюнкцию раскрывают по дизъюнкции. Все это мы сейчас проделаем на примере.
, которая равна 0 и на дизъюнкцию не влияет. Затем эту конъюнкцию раскрывают по дизъюнкции. Все это мы сейчас проделаем на примере.
Как и прежде, образуем конъюнкцию p (p ® q) и приводим ее к СКНФ. Освобождаемся от импликации: p (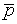 + q). B дизъюнкте p не хватает члена q. Прибавляем конъюнкцию
+ q). B дизъюнкте p не хватает члена q. Прибавляем конъюнкцию 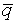 Ù q:
Ù q:
(p + (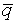 Ù q))(
Ù q))(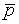 + q). Раскрывая эту конъюнкцию, получаем СКНФ:
+ q). Раскрывая эту конъюнкцию, получаем СКНФ:
(p + q) Ù (p + 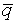 ) Ù (
) Ù (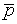 + q). Полученная СКНФ дает нам не только три конъюнктивных члена: (p + q), (p +
+ q). Полученная СКНФ дает нам не только три конъюнктивных члена: (p + q), (p + 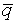 ) и (
) и (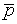 + q), каждый из которых является логическим следствием, но и возможность получать другие следствия в виде конъюнкции любой пары из них:
+ q), каждый из которых является логическим следствием, но и возможность получать другие следствия в виде конъюнкции любой пары из них:
(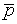 + q) Ù (p +
+ q) Ù (p + 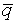 ), (p + q) Ù (
), (p + q) Ù (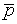 + q), (p + q) Ù (p +
+ q), (p + q) Ù (p + 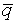 ).
).
Но и это еще не все следствия. Применяя метод резолюций, получаем дополнительно дизъюнкты: p и q (Проверить самостоятельно).
Пример 2. Институт заключает договор, в котором предположительно могут участвовать три кафедры А, М и R. Однако участие этих кафедр обусловливается рядом обстоятельств. А именно:
а) если М не участвует в договоре, то не участвует и А;
б) если же М участвует, то участвуют и А, и R.
Но вот вопрос: обязана ли R участвовать в договоре, если в нем уже участвует А?
Опишем задачу в терминах исчисления высказываний. Обозначим: a – в договоре участвует А, m - в договоре участвует М, и r – в договоре участвует R. Тогда условию а) соответствует формула 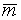 ®
® 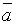 , условию б): m ® (a Ù r). Необходимо решить, следует ли из этих условий a ® r?
, условию б): m ® (a Ù r). Необходимо решить, следует ли из этих условий a ® r?
Требуется вывести логическое следствие:
((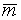 ®
® 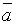 ), (m ® (a Ù r))
), (m ® (a Ù r)) 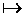 (a ® r).
(a ® r).
Исключаем импликации и делаем небольшие преобразования:
[(m+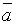 ), (
), (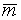 + ar)]
+ ar)] 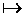 (
(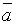 + r),
+ r),
[(m+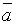 ), ((
), ((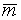 + a)(
+ a)(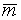 + r))]
+ r))] 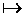 (
(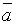 + r),
+ r),
[(m+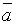 ), (
), (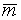 + a), (
+ a), (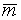 + r)]
+ r)] 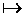 (
(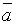 + r),
+ r),
Согласно принципу дедукции, требуется доказать условие:
[(m + 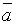 ), (
), (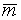 + a), (
+ a), (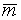 + r) ,
+ r) ,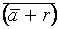 ]
] 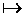 Л.
Л.
Применяя метод резолюции, анализируем:
дизъюнкты: резолюции:
1. m +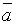 , 6. m, (1,4)
, 6. m, (1,4)
2. 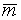 + a, 7. r, (3,6)
+ a, 7. r, (3,6)
3. 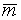 + r, 8. Л. (5,7)
+ r, 8. Л. (5,7)
4. a, Кафедра R обязана участвовать
5. 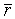 . в договоре, если участвует А.
. в договоре, если участвует А.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 519; Нарушение авторских прав?; Мы поможем в написании вашей работы!