Отсечение

Жидкая частица – часть жидкости, малая по сравнению с объемом рассматриваемой жидкости, и в то же время объем частицы велик по сравнению с объемом молекулы жидкости. В частице содержится так много молекул, что жидкость в пределах частицы можно считать сплошной средой – континуумом.

Ряд интеграл Фурье.

Определение периодической функции:

, (1)

где Т – период; n – любое целое числа положительное или отрицательное.

Определение (1) выражает основное св-во периодичности функции, состоящее в том, что ход явления периодически повторяется и периодичность эта существует для всех времён от + до - То есть периодических явлений в действительности нет.

Периодическая функция есть полезная математическая абстракция:

, (2)

Формула представлена в виде 2х слагаемых. Значение и должны быть подобраны таким образом, чтобы равенство (2) выполнялось.

Частоты колебаний, из которых составляется периодическая функция, образуют гармоническую последовательность. Отдельные составляющие носят название гармоники колебания.

Выражение (2) часто употребляется в другой форме:

, (3)

,,

,

, (4)

(5)

Величина выражает среднее значение функции за период, она наз-ся постоянной составляющей. Выражается: (6)

Замечательным свойством ряда Фурье яв-ся то, что есть взять конечное число членов ряда и представить в виде: то для любого N получается наименьшее квадратное отклонение от точного значения.

С увеличением числа членов N приближение улучшается в пределе и если N в пределе стремится к бесконечности, то приближение становится точным.

Ряд Фурье в комплексной форме:

, (7)

где;.

Величина есть комплексная амплитуда и выражается по формуле: (8).

Наглядный путь к получению разложения Фурье не периодической функции состоит в применении перехода. Для этого возьмём формулу (7) и подставим в неё значение из формулы (8):.

Сделаем следующую замену последующей схеме:

текучая частота, изменяющаяся непрерывно; её приращение.

(9);

(10); - интеграл Фурье в комплексной форме.

(11).

Комплексная амплитуда каждого отдельного колебания бесконечно мала и равна:.

Частотный интервал бесконечно мал и равен.

В общем случае движение жидкости можно считать определенным, если известны законы движения всех частиц, то есть положение каждой частицы задано как функция времени.

2. ДВА МЕТОДА ИЗУЧЕНИЯ ДВИЖЕНИЯ ЖИДКОСТИ

Для удобства исследования любой жидкости объем можно представить состоящим из большого числа жидких частиц. В соответствии с этим к исследованию движения жидкой частицы возможен такой же подход, как и к исследованию движения точки в механике. При этом частицу отождествляют с материальной точкой, рассматриваемой в теоретической механике.

Такой подход получил название метода Лагранжа (рис. 4.1).

В начальный момент времени выделим в жидкости фиксированную частицу с координатами x₀, y₀, z₀. Движение этой частицы известно, если известны законы изменения координат, характеризующих положение частицы с течением времени:

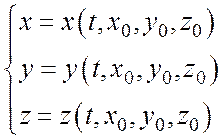(4.1)

Исключая из этих уравнений время t, получим уравнение траектории, то есть след движения частицы в пространстве. Переменные x ₀, y ₀, z ₀ и t называют переменными Лагранжа.

Проекции скоростей частиц жидкости определяются зависимостями:

,

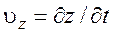где – рассматриваются как параметры, а ускорения – зависимостями

.

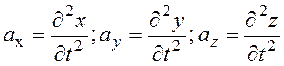Для описания движения жидкого объема, содержащего N частиц, следует задать соответствующее число систем уравнений типа (4.1), что создает большие математические трудности.

В чистом виде метод Лагранжа используется редко. Он позволяет проследить за движением любой фиксированной частицы, однако это излишне, поскольку все частицы практически одинаковы. Метод Лагранжа находит применение при решении ряда специальных задач, например волновых движений.

Широкое применение для исследования получил метод Эйлера (рис. 4.2). По этому методу рассматривают поле скоростей в точках пространства, занятого движущейся жидкостью, и исследуют характер изменения скорости в этих точках в зависимости от времени. Под скоростью в точке пространства понимают скорость жидкой частицы, которая в данный момент времени находится в этой точке. Поле скоростей по этому методу создается в виде:

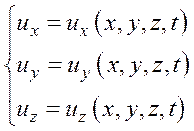
или

,

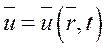где 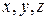– координаты точки пространства, а не жидкой частицы.

Скорость u называется мгновенной местной скоростью. Совокупность мгновенных местных скоростей представляет собой векторное поле, называемое полем скоростей. В общем случае поле скоростей может изменяться во времени и по координатам. Переменные x, y, z, t называют переменными Эйлера.

Как известно, чтобы задать движение твердого тела, необходимо знать скорости трех его точек (не лежащих на одной прямой). Если же нужно задать движение жидкости, то есть тела легко деформируемого, требуется знать скорость во всех точках занимаемого пространства. Число этих точек в пределе стремиться к бесконечности.

Метод Эйлера проще метода Лагранжа, так как в нем используется хорошо разработанный математический аппарат теории поля. Применяя метод Эйлера, который не позволяет учесть индивидуальность каждой частицы, следят за поведением различных частиц, проходящих через фиксированную точку пространства.

3. ЛИНИЯ ТОКА И ЭЛЕМЕНТАРНАЯ СТРУЙКА

С методом Эйлера тесно связано понятие линии тока. Выделим в потоке в фиксированный момент времени ряд точек. Проведем линию, касательные к которой совпадали бы с направлением векторов скорости жидких частиц, находящихся в этих точках. Эта линия называется линией тока (рис. 4.3).

Иными словами линия тока касательная к векторам скоростей. Она соединяет отдельные жидкие частицы в один и тот же момент времени, чем существенно отличается от траектории, представляющей след движения одной частицы.

Траекторией называется путь, проходимый данной частицей жидкости в пространстве за определенный промежуток времени. При установившемся движении форма траекторий не изменяется во время движения. При неустановившемся движении непрерывно изменяются и величины, и направления скорости движения. Траектории движения частиц в этом случае также непрерывно изменяются во времени.

Получим дифференциальные уравнения линий тока, учитывая, что их векторный элемент 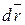совпадает с направлением вектора скорости 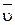, то есть ||.

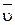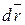Воспользовавшись тем, что векторное произведение двух векторов равно нулю, запишем дифференциальное уравнение линии тока в векторном виде:

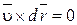
Раскрывая векторное произведение, получим

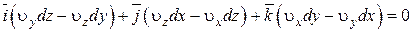
или, приравнивая множители при ортах нулю,

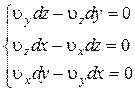
Поделив первый член этой системы на , второй на 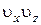, третий на 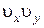, представим ее в виде

Это соотношение может быть записано более компактно:

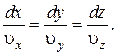
Необходимо иметь в виду различие между траекторией частицы жидкости и линией тока. В то время как траектория относится лишь к одной определенной частице жидкости и показывает путь, проходимый этой частицей в пространстве за некоторый промежуток времени, линия тока связывает между собой различные лежащие на ней частицы и характеризует направление их движения в данный момент времени.

Линии тока соответствуют состоянию поля скоростей в движущейся жидкости в данный момент времени. Если в следующий момент поле скоростей изменится, то изменится и положение линий тока.

Однако в случае установившегося движения, характеризуемого неизменяемостью поля скоростей во времени, частицы жидкости будут следовать вдоль неизменных линий тока; таким образом, линии тока и траектории частиц жидкости совпадают между собой только при установившемся движении.

Линии тока и траектории можно сделать видимыми, чем широко пользуются в лабораторной практике при различного рода экспериментальных исследованиях и наблюдениях над движением жидкости. Для этого, например, на поверхности жидкости рассеивают мелкие частицы какого-нибудь вещества, нерастворимого в жидкости, и при помощи фотографического аппарата производят съемку. При съемке с короткой выдержкой эти частицы дают на пластинке короткие черточки (штрихи), которые при достаточно большом количестве частиц сливаются и показывают общую картину линий тока (рис. 4.4).

Введем понятие трубки тока. Выделим в жидкости замкнутый контур, не являющийся линией тока. Через каждую точку этого контура проведем линию тока и получим трубчатую поверхность тока – трубку тока. Жидкость, заключенная внутри контура тока, называется жидкой струйкой. В общем случае скорости жидкости по поперечному сечению струйки различны. Элементарной называют жидкую струйку, в которой можно пренебречь изменением скорости по ее поперечному сечению.

4. КЛАССИФИКАЦИЯ ПОТОКОВ ЖИДКОСТИ

Рассмотрим зависимость поля скоростей потока от времени (признак классификации).

Установившимся называют такое движение, при котором скорость потока в любой точке пространства не зависит от времени.

В противном случае движение жидкости называется неустановившимся.

Поле скоростей при установившемся движении не зависит от времени.

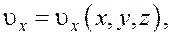
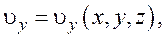
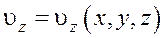
или

Если рассмотреть определенную точку пространства с координатами 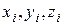, через которую с течением времени проходят различные частицы жидкости, то все они обладают одинаковой скоростью вне зависимости от времени. Но в разных точках пространства скорости различны, и поля скоростей неоднородны.

При установившемся движении жидкости траектории и линии тока совпадают.

Рассмотрим частицу жидкости, находящуюся в момент времени 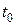в точке А (рис. 4.5). Линия АВС есть линия тока в момент времени 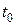. За время частица переместится по касательной к вектору скорости 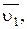в точку В вдоль линии тока. В точке В величина скорости через время останется неизменной как по величине, так и по направлению, вследствие чего частица жидкости будет передвигаться далее в точку С вдоль линии тока. Повторяя далее эти рассуждения, убеждаемся, что траектория частицы, в начальный момент времени занимавшей точку А, будет при установившемся движении совпадать с линией тока.

При неустановившемся движении скорость в точке В в момент времени 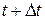изменится по величине и направлению, и частица жидкости, попав в эту точку, в дальнейшем будет двигаться по касательной к новой, измененной скорости, сойдя с Ли­нии АВС, являвшейся лини­ей тока в момент времени .

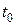Рассмотрим классификацию потоков жидкости по их геометрическим признакам.

Введем понятие пространственного, плоскопараллельного и осесимметричного течения жидкости. Методы исследований этих течений в ряде случаев различны.

Пространственное (трехмерное) движение характеризуется тем, что поле скорости в нем зависит от трех декартовых координат .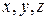

В соответствии с этим в пространственном течении имеются три проекции скорости на оси координат:

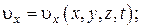
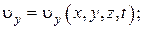
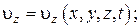
Плоскопараллельным называется такое движение жидкости, при котором картины течения в плоскостях, перпендикулярных некоторой оси, одинаковы.

В сходственных точках, лежащих в параллельных плоскостях, скорости одинаковы и не зависят от координаты .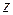

Иными словами

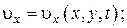
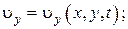
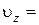0.

Следовательно, при изучении плоскопараллельного движения можно ограничиться исследованием течения только в плоскости ; это случай решения плоской задачи гидромеханики. В чистом виде плоскопараллельное движение не наблюдается.

Осесимметричным называется движение жидкости, при котором поле скорости одинаково в любых плоскостях, проходящих через некоторую прямую, называемую осью симметрии потока.

5. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ

Любой поток должен удовлетворять закон сохранения массы. Уравнение сплошности или неразрывности представляет собой гидромеханическое выражение закона сохранения массы.

Рассмотрим жидкую частицу объемом V (рис. 4.6). Ее масса равна 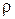V. Согласно закону сохранения материи, производная от массы этой частицы

.

Взяв производную и разделив результат на массу 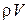, получим

.

Полагая жидкость несжимаемой и однородной , придем к следующему математическому выражению для закона сохранения материи:

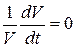. (4.2)

Из этого выражения следует, что для несжимаемой жидкости закон сохранения массы переходит в закон сохранения объема частиц. Величина 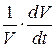представляет собой относительную скорость изменения объема. Для этого рассмотрим жидкую частицу, первоначально имевшую форму шара радиуса 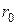. Размеры частицы предполагаем малыми. Предположим, что оси декартовых координат совпадают с главными осями деформации. Под их воздействием сфера деформируется в эллипсоид. Если - относительная скорость линейных деформаций, то выражение для полуосей эллипсоида 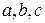через элементарное время деформации 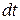можно записать в виде:

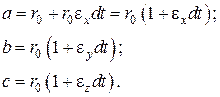(4.3)

Начальный объем частицы - 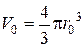, а конечный, после деформации - .

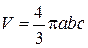Приращение объема 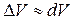с учетом (4.3) составит

.

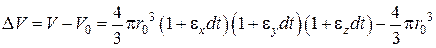Ограничиваясь малыми первого порядка, находим

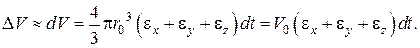
Подставляя полученное выражение в закон сохранения массы (4.2), получим

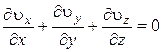. (4.4)

Сумма 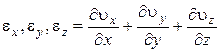называется относительной скоростью объемного расширения, согласно (4.4), у несжимаемой жидкости равна нулю. То есть объем частицы до и после деформации не изменяется.

Зависимость (4.4) можно представить в виде

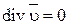. (4.5).

Выражения (4.4)и (4.5) представляют собой уравнения неразрывности в дифференциальной форме.

Получим интегральную форму уравнения неразрывности.

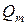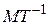Предварительно введем понятие расхода жидкости через поверхность, понимая под ним количество жидкости, протекающее в единицу времени через незамкнутую поверхность. Различают объемный расход Q (размерность ), массовый расход () и весовой расход ().

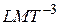Между этими величинами в однородной жидкости существует соотношение:

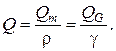
В дальнейшем будем оперировать понятием объемного расхода. Для получения общего выражения расхода рассмотрим течение жидкости через поверхность S. Выделим на ней элементарную площадку 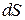. Вектор скорости в центре площадки разложим на нормальную 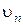и касательную _τ составляющие. Очевидно, касательная составляющая _τ не дает расхода жидкости через площадку. За время 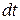через 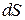протечет объем жидкости 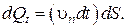Элементарный расход будет равен отношению 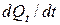(количество жидкости, отнесенное к единице времени), то есть

.

Суммируя расходы по элементарным площадкам, что сведено к интегрированию по поверхности, получим выражение для расхода жидкости через поверхность S:

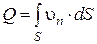(4.6)

Выделим в жидкости поверхность S произвольного объема V. Возьмем элементарный объем 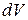и умножим его на .

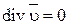Физически количество 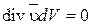характеризует, согласно (4.2) 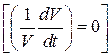, изменение величины элементарного объема 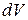вследствие деформации. Проинтегрируем количество 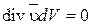по объему и воспользуемся формулой Гаусса – Остроградского, переводящей объемный интеграл в поверхностный.

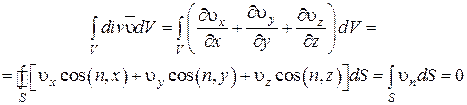(4.7)

В этой формуле введена нормальная составляющая скорости 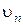. Согласно (4.6) 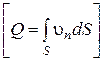, интеграл в правой части представляет собой расход жидкости через замкнутую поверхность, равный в соответствии с (4.7)

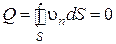. (4.8)

Это выражение представляет математическую формулировку уравнения неразрывности в интегральной форме. Физически оно истолковывается следующим образом: расходы втекающей и вытекающей жидкости через произвольную замкнутую поверхность должны быть равны. При этом внутри жидкости не происходит ни накопления жидкости, ни образования пустот.

Живым сечением потока называется поверхность, нормальная к векторам скоростей. Если S поверхности живого сечения, то расход через нее выражается как

.

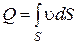Введем среднюю по живому сечению скорость. Под ней понимается фиктивная, постоянная по живому сечению скорость 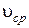, обеспечивающая одинаковый с заданным расход. Из этого определения следует, что

.

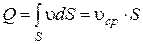Средняя скорость равна расходу, деленному на площадь живого сечения:

.

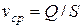Рассмотрим поток жидкости (рис. 4.7) конечных размеров, ограниченный с боков твердыми стенками 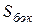. Проведем два произвольных живых сечения 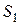и 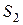. Расход жидкости через замкнутую поверхность , согласно предыдущим выводам, равен нулю.

Рис. 4.7. Поток жидкости

Считая поток вытекающей жидкости положительным, а втекающей – отрицательным, запишем

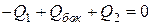
и поскольку 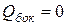, то , то есть расход жидкости вдоль потока конечных размеров постоянен. С учетом введения понятия средних скоростей последнее равенство может быть записано в виде:

.

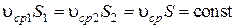Уравнение неразрывности в такой форме находит широкое применение при исследовании течений жидкости.

6. АНАЛИЗ ДВИЖЕНИЯ ЖИДКОЙ ЧАСТИЦЫ

Классификация движений жидкости на основании зависимости скоростей потока от времени позволяет дать лишь внешнее описание их особенностей. Чтобы выявить внутренние особенности течения, необходимо исследовать распределение скоростей внутри жидкой частицы. Это позволит судить о ее движении в целом.

При рациональном методе исследования какого-либо явления его сравнивают с другим, более простым явлением, определяя особенности более сложного явления по сравнению с простым.

Сравним движение жидкой частицы с известным из теоретической механики движением абсолютно твердого тела. Движение жидкой частицы носит более сложный характер, поскольку она в отличие от твердого тела может деформироваться, причем очень значительно по сравнению с упругим телом.

В курсе теоретической гидромеханики аналитически показано, что

,

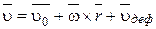то есть скорость любой точки жидкой частицы складывается из скорости полюса , скорости вращения вокруг собственной оси, проходящей через полюс 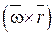и скорости деформированного движения .

Это положение представляет собой формулировку теоремы Коши – Гельмгольца.

Впервые полеченная формула отличается от аналогичной формулы для твердого тела только наличием члена .

Однако член, характеризующий вращение 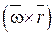лишь по форме совпадает с аналогичным членом для твердого тела. Жидкая частица с течением времени деформируется, изменяет свою форму. Поэтому член 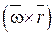описывает вращение жидкой частицы как отвердевшего тела лишь в данный момент времени, так как по прошествии этого времени она изменяет свою форму.

Дальнейший анализ формулы Коши – Гельмгольца показывает, что в произвольном случае движения жидкости скорость можно представить в виде суммы двух слагаемых, одно из которых является потенциальным вектором, а другое имеет вихревую природу:

,

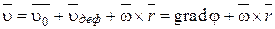где .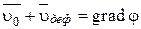

Если угловые скорости вращения равны нулю, то скорость является потенциальным вектором:

.

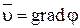Подобное движение образует класс безвихревых или потенциальных движений.

Если 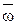не равно нулю, движение жидкости называется вихревым.

Таким образом, на основании формулы Коши – Гельмгольца, все течение жидкости можно разделить на вихревое и потенциальное. Методы исследования этих течений существенно различаются.

7. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
ВИХРЕВОГО ДВИЖЕНИЯ ЖИДКОСТИ

Вихревым называется такое движение жидкости, при котором вектор угловой скорости 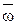отличен от нуля.

Вихревой линией называют линию, в каждой точке которой в данный момент времени вектор угловой скорости совпадает с касательной к этой линии.

Дифференциальное уравнение вихревой линии:

,

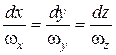где dx, dy, dz - проекции элемента вихревой линии;

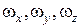- проекции угловой скорости.

Аналогично понятию трубки тока вводится понятие вихревой трубки.

Вихревая трубка - часть жидкости, ограниченная вихревыми линиями, проведенными через точки произвольного замкнутого контура.

Элементарной вихревой трубкой называют такую, для которой применением угловой скорости по искомому сечению можно пренебречь.

Воздействие вихревой трубки на окружающую жидкость характеризуется ее интенсивностью.

Под интенсивностью вихревой трубки понимается удвоенный поток вектора угловой скорости через произвольные поперечные сечения вихревой трубки:

.

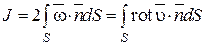Можно показать, что - интенсивность элементарной вихревой трубки.

.

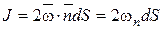Введем фундаментальное в гидромеханике понятие циркуляции скорости Г. Она представляет собой криволинейный интеграл по замкнутому контуру L от скалярного произведения вектора скорости 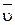на дифференциал радиус-вектора точки контура .

.

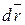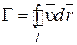Связь между интенсивностью и циркуляцией устанавливается теоремой Стокса. Формулируется эта теорема так: поток вектора вихря через произвольную замкнутую поверхность равен циркуляции скорости по контуру, на который опирается эта поверхность.

Смысл теоремы состоит в том, что интенсивность вихревой трубки равна циркуляции скорости по контуру, на который опирается площадь поперечного сечения трубки:

.

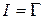Понятие интенсивности и циркуляции является чисто кинематическими, следовательно, теорема Стокса одинаково справедлива для течения как вязкой, так и невязкой жидкости.

Пример. Давайте создадим предикат, который будет находить максимум из двух чисел. У предиката будет три аргумента. Первые два аргумента - входные для исходных чисел, в третий выходной аргумент будет помещен максимум из первых двух аргументов.

Предикат будет довольно простым. Мы запишем, что в случае, если первое число больше второго, максимальным будет первое число, в случае, если первое число меньше, максимумом будет второе число. Надо также не забыть про ситуацию, когда числа равны, в этом случае максимумом будет любое из них.

Решение можно записать в следующем виде:

max(X,Y,X):-

X>Y. /* если первое число больше второго,

то первое число - максимум */

max(X,Y,Y):-

X<Y. /* если первое число меньше второго,

то второе число - максимум */

max(X,Y,Y):-

X=Y. /* если первое число равно второму,

возьмем в качестве максимума

второе число */

Первое предложение можно объединить со вторым или третьим в одно предложение. Тогда процедура будет состоять не из трех предложений, а всего из двух:

max(X,Y,X):-

X>Y. /* если первое число больше второго,

то первое число - максимум */

max(X,Y,Y):-

X<=Y./* если первое число меньше или равно

второму, возьмем в качестве максимума

второе число */

Однако полученная процедура еще далека от совершенства. С одной стороны, в случае, когда первое проверяемое условие (X>Y) не выполнено, будет проверяться второе условие (X<=Y), хотя понятно, что если не выполнено X>Y, значит X<=Y. С другой стороны, в случае, если первое условие имело место и первое число оказалось больше второго, Пролог-система свяжет третий аргумент предиката max с первым аргументом, после чего попытается сопоставить второе предложение. Хотя нам очевидно, что после того, как максимум определен, не нужно больше ничего делать. Других вариантов в данной ситуации просто не может быть. И, значит, проверка второго условия избыточна.

В данной ситуации нам пригодится встроенный предикат, который по-английски называется cut, по-русски - отсечение, а в программе на Прологе он обозначается восклицательным знаком "!". Этот предикат предназначен для ограничения пространства поиска, с целью повышения эффективности работы программ. Он всегда завершается успешно. После того, как до него дошла очередь, он устанавливает "забор", который не дает "откатиться назад", чтобы выбрать альтернативные решения для уже "сработавших" подцелей. То есть для тех, которые расположены левее отсечения. На цели, расположенные правее, отсечение не влияет. Кроме того, отсечение отбрасывает все предложения процедуры, расположенные после предложения, в котором находится отсечение.

С использованием отсечения наше решение будет еще короче:

max2(X,Y,X):-

X>Y,!./* если первое число больше второго,

то первое число - максимум */

max2(_,Y,Y). /* в противном случае максимумом будет

второе число */

В случае, если сработает отсечение, а это возможно, только если окажется истинным условие X>Y, Пролог-система не будет рассматривать альтернативное второе предложение. Второе предложение "сработает" только в случае, если условие оказалось ложным. В этой ситуации в третий аргумент попадет то же значение, которое находилось во втором аргументе. Обратите внимание, что в этом случае нам уже не важно, чему равнялся первый аргумент, и его можно заменить анонимной переменной.

Все случаи применения отсечения принято разделять на "зеленые" и "красные". Зелеными называются те из них, при отбрасывании которых программа продолжает выдавать те же решения, что и при наличии отсечения. Если же при устранении отсечений программа начинает выдавать неправильные решения, то такие отсечения называются красными.

Пример "красного" отсечения имеется в реализации предиката max2 (если убрать отсечение, предикат будет выдавать в качестве максимума второе число, даже если оно меньше первого). Пример "зеленого" отсечения можно получить, если в запись предиката max добавить отсечения (при их наличии предикат будет выдавать те же решения, что и без них).

В принципе, с помощью отсечения в Прологе можно смоделировать такую конструкцию императивных языков, как ветвление.

Процедура

S:-

<условие>,!,P.

S:-

P2.

будет соответствовать оператору if <условие> then P else P2, то есть если условие имеет место, то выполнить P, иначе выполнить P2. Например, в случае с максимумом, можно расшифровать нашу процедуру как "если X>Y, то M=X, иначе M=Y ".

Пример. Теперь напишем предикат, который будет находить максимум не из двух чисел, а из трех. У него будет уже четыре параметра. Первые три - входные для сравниваемых чисел, а четвертый - выходной параметр для их максимума.

Подходов к решению этой задачи может быть несколько.

Первое, что приходит в голову, это решить задачу по аналогии с нахождением максимума из двух чисел. Вариант без отсечения будет выглядеть так:

max3a(X,Y,Z,X):-

X>=Y,X>=Z.

/* если первое число больше или равно второму

и третьему, то первое число - максимум */

max3a(X,Y,Z,Y):-

Y>=X,Y>=Z.

/* если второе число больше или равно первому

и третьему, то второе число является

максимумом */

max3a(X,Y,Z,Z):-

Z>=X,Z>=Y.

/* если третье число больше или равно первому

и второму, то максимум - это третье число */

Недостаток этой программы, кроме ее длины, еще и в том, что если какие-то из исходных чисел окажутся равными, мы получим несколько одинаковых решений. Например, если все три числа совпадают, то каждое из трех правил будет истинным и, соответственно, мы получим три одинаковых, хотя и правильных ответа.

Применение отсечения позволит существенно сократить решение:

max3b(X,Y,Z,X):-

X>Y,X>Z,!.

/* если первое число больше второго и третьего,

то первое число - максимум */

max3b(_,Y,Z,Y):-

Y>=Z,!.

/* иначе, если второе число больше третьего,

то второе число является максимумом */

max3b(_,_,Z,Z). /* иначе максимум - это третье число */

Число сравнений значительно сократилось за счет того, что отсечение в первом правиле гарантирует нам, что на второе правило мы попадем только в том случае, если первое число не больше второго и третьего. В этой ситуации максимум следует искать среди второго и третьего чисел. Если ни первое, ни второе число не оказались больше третьего, значит, в качестве максимума можно взять как раз третье число, уже ничего не проверяя. Обратите внимание на то, что во втором правиле нам было не важно, чему равно первое число, а в третьем предложении участвовало только третье число. Не участвующие параметры заменены анонимными переменными.

И, наконец, самое короткое решение можно получить, если воспользоваться уже имеющимся предикатом max2. Решение будет состоять всего из одного предложения.

max3(X,Y,Z,M):-

max2(X,Y,XY), /* XY - максимум из X и Y */

max2(XY,Z,M). /* M - максимум из XY и Z */

Мы записали, что для того, чтобы найти максимум из трех чисел, нужно найти максимум из первых двух чисел, после чего сравнить его с третьим числом.

Дата добавления: 2014-01-05