Додатні раціональні числа як нескінченні періодичні десяткові дроби. Чисті та мішані періодичні дроби та їх перетворення у звичайні

9. У попередньому пункті ми довели теорему, яка визначила умови, при яких звичайний дріб перетворюється у десятковий. Цілком закономірно виникає запитання «а як бути у випадках, коли знаменник у канонічному розкладі містить прості множники, відмінні від 2 і 5?». Розглянемо звичайний дріб 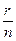такий, що n=2^m•5^k•р, де р – простий множник, відмінний від 2 і 5. На практиці при спробі перетворити такі звичайні дроби у десяткові шляхом ділення чисельника на знаменник доводиться зустрічатися з двома випадками: 1) на певному кроці ділення одна цифра чи група цифр починає повторюватися одразу після коми; 2) на певному кроці ділення одна цифра чи група цифр починає повторюватися не одразу після коми. Наприклад, =0,232323…; 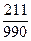=0,2131313…. В таких випадках говорять, що дістаємо нескінченний періодичний десятковий дріб.

Означення: нескінченний десятковий дріб, у якого одна цифра або група цифр весь час повторюється називається нескінченним періодичним дробом.

Означення: одна цифра або група цифр, яка повторюється, називається періодом.

Нескінченні періодичні дроби прийнято позначати так: 0,2131313…=0,2(13), 0,373373373…=0,(373). Число, утворене цифрами, що стоять після коми до періоду, називають доперіодичною частиною. У наведених прикладах: (13) і (373) – це періоди, а число 2 у першому дробові – доперіодична частина. В математиці доведено, що число цифр у періоді нескінченного періодичного дробу не перевищує n-1, де n знаменник звичайного дробу 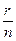. Серед нескінченних періодичних дробів виділяють чисті та мішані періодичні дроби.

Означення: чистим періодичним дробом називається нескінченний десятковий дріб, у якого період починається одразу після коми.

Означення: мішаним періодичним дробом називається нескінченний десятковий дріб, у якого період починається не одразу після коми.

Таким чином, ми з’ясували, що при перетворенні звичайних дробів у десяткові, ми можемо зустрітися з двома випадками: 1) ділення чисельника на знаменник призводить до скінченного десяткового дробу; 2) ділення чисельника на знаменник призводить до нескінченного десяткового дробу, в якому одна цифра чи група цифр весь час повторюється. Отже, можна стверджувати, що нескінченні періодичні дроби існують. У зв’язку з цим виникає питання про перетворення чистих і мішаних періодичних дробів у звичайні. У математиці доведені теореми, на яких ґрунтуються наступні правила перетворення періодичних дробів у звичайні.

Правило 1: чистий періодичний десятковий дріб дорівнює звичайному дробові, чисельником якого є число, що стоїть у періоді, а знаменником – число, яке записане стількома дев’ятками, скільки цифр у періоді.

Правило 2: мішаний періодичний десятковий дріб дорівнює звичайному дробові, чисельник якого є різниця між числом, що стоїть після коми до кінця періоду, та числом, що стоїть після коми до періоду, а знаменником є число, яке записане стількома дев’ятками, скільки цифр у періоді, та стількома нулями, скільки є цифр до періоду.

Вправа: перетворити періодичні дроби у звичайні: 0,(243); 0, 134(27).

Дата добавления: 2014-01-05