Два подхода к разработке сетевых графиков

Терминология

Конструирование сетевого графика проекта

Операция (или работа). Для руководителей проектов операция - это неделимый элемент проекта, требующий затрат времени для своего выполнения.

Обычно выполнение операций связано с затратами времени и трудовых ресурсов.

Иногда это может быть просто время. Примерами этого могут быть операция ожидания подписания контракта или ожидание поступления материалов, одобрения правительства, таможенное оформление грузов и т.д.

Операции обычно состоят из одной или более работ из наборов работ. Как правило, название операциям дается в повелительной форме глагола, например, "разработать спецификацию продукта".

Операция слияния. Это операция, которая имеет более одной непосредственно предшествующей ей операции.

Параллельные операции. Это операции, которые могут, по желанию менеджера, выполняться одновременно. Однако совсем не обязательно осуществлять параллельные операции одновременно.

Путь. Последовательность связанных, взаимозависимых операций.

Критический путь. Это самый длинный путь во всей системе операций; если выполнение операции на этом отрезке задерживается, выполнение всего проекта задерживается на такое же время.

Событие. Термин используется для обозначения точки времени начала или завершения операции. Событие не требует времени.

Дробящаяся операция. Это операция, за которой сразу следуют несколько операций (от нее исходит более одной стрелки, обозначающей зависимость).

Для разработки сетевых графиков могут применяться два подхода:

подход с обозначением операций в узлах (блоках) графика - ОУ;

подход с обозначением операций на стрелках графика - ОС.

На практике первый метод - ОУ - используется значительно чаще и далее излагается именно этот метод.

Основные правила разработки сетевого графика

При разработке сетевого графика целесообразно придерживаться следующих 8 правил:

Сетевой график разворачивается слева направо.

Ни одна операция не может быть начата, пока все предшествующие связанные с ней операции не будут выполнены.

Стрелки в сетевом графике отображают отношения предшествования и следования. На рисунке стрелки могут пересекаться.

Каждая операция должна иметь свой собственный номер.

Номер последующей операции должен быть больше номера любой предшествующей операции.

Образование петель недопустимо (другими словами, не должно происходить зацикливания хода выполнения установленного набора операций).

Условные переходы от одной операции к другой не допускаются (имеется в виду определение последовательности хода выполнения операций условиями типа: "Если будет достигнут успех, сделайте то-то...; если нет - ничего не предпринимайте").

Опыт показывает, что когда существует несколько исходных операций проекта, то может быть определен общий узел начала всего комплекса работ. Точно так же один узел может быть использован для четкого обозначения окончания проекта.

Принципы построения и анализа сетевых графиков типа "ОУ"

Рис. 10.3 дает несколько типичных конструкций сетевого графика, построенного этим методом ОУ.

Операция представлена в виде блока. Блок может иметь различные формы, но в последнее время блок чаще всего представляют в виде прямоугольника.

Зависимость между операциями показывается на графике стрелками между прямоугольниками (блоками).

Стрелки показывают, как операции связаны между собой и последовательность их выполнения.

На практике операциям соответствуют определенные номера и краткое описание.

При включении любой операции в сетевой график необходимо определить для нее три отношения. Эти отношения могут быть определены в результате ответов на следующие три вопроса:

Какие операции должны быть завершены непосредственно перед этой операцией? Эти операции называются предшествующими по отношению к данной.

Какие операции должны следовать непосредственно за этой операцией? Эти операции называются следующими за данной.

Какие операции могут выполняться во время выполнения этой операции? Какие операции можно назвать параллельными данной?

Такая информация позволяет аналитикам конструировать графические схемы последовательности и логической взаимозависимости любых операций проекта.

Рис. 10.3 (А) дает пример того, какие действия должны выполняться после того, как что-то уже сделано. Такой график показывает менеджеру проекта, что операция А должна быть выполнена до начала операции В, а операция В должна быть завершена до начала операции С.

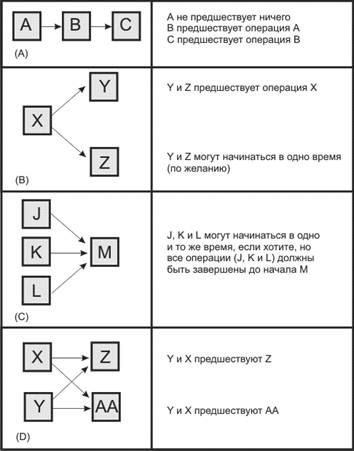
Типичные конструкции сетевого графика, построенного методом ОУ

Рис. 10.3(В) показывает, что операции Y и Z не могут быть начаты, пока не завершена операция X. Этот рисунок также показывает, что операции Y и Z могут происходить параллельно или одновременно, по желанию менеджера, но это не обязательное условие. Например, заливка бетоном дороги (операция Y) может происходить во время процесса укладки газона (операция Z), но уборка территории (операция X) должна быть завершена до начала операций Y и Z. Операции Y и Z считаются параллельными.

Рис. 10.3(С) показывает, что операции J,K,L при желании могут происходить одновременно, а операция М не может быть начата, пока операции J,K,L не будут завершены. Операции J, К, L параллельны.

В рис. 10.3(D) операции Y и X параллельны и могут происходить одновременно; операции Z и АА также параллельны. Но операции Z и АА нельзя начинать, пока обе операции X и Y не завершены.

Зная эти основы построения сетевых графиков методом ОУ, мы можем попробовать разработать простую сеть.

Информация для упрощенной сети проекта нового бизнес-центр дана в табл. 10.1.

Таблица 10.1. Информация для сетевого графика Бизнес-центр Колла

Операция	Описание	Предшествующая операция
А	Утверждение приложения	Нет
В	Планы конструирования	А
С	Изучение трафика	А
D	Проверка наличия службы	А
Е	Отчет персонала	B,C
F	Утверждение на комиссии	В, C, D
G	Ожидание работ	F
Н	Включение в работу	E,G

Операции А (одобрение заявки) ничего не предшествует, следовательно, она является первым блоком, который нужно нарисовать. Далее, отметим, что операциям В, C, и D (планы строительства, изучение движения и наличия рынка услуг) предшествует операция А

Рис. 10.4. Сетевой график разработки бизнес-центра Колла

Мы рисуем три стрелки и соединяем их с операциями В, C, и D. Этот сегмент показывает руководителю проекта, что операция А должна быть завершена до начала операций В, C и D. После завершения А, операции В,C, и D могут при желании проходить параллельно. рис. 10.4 показывает сеть полностью со всеми операциями.

Оценка начала и окончания работ с помощью сетевого графика

Реальный план проекта и сетевой график требуют надежной оценки времени всех операций проекта.

Внесение времени в сетевой график позволяет оценить продолжительность осуществления проекта.

Сетевой график проекта с оценкой продолжительности операций связывает в систему планирование, составление расписания и контроль проектов.

Дата добавления: 2014-01-05