Уширение давлением

Уширение спектральных линий, связанное с взаимодействием излучающей атомной системы с окружающей средой, носит общее название “ уширение давлением ”. При сближении с другими частицами происходит изменение силового поля в окрестности возбужденного атома и, следовательно, происходит изменение энергии электронных термов. В этом разделе, исходя из простейшей теории возмущения классического осциллятора окружающими частицами, будут очень кратко изложены основные понятия теории уширения давлением в объеме минимально необходимом для понимания процессов в низкотемпературной плазме.

В большинстве случаев в низкотемпературной плазме основную роль играют парные столкновения. Гамильтониан атома изменяется при столкновении на величину

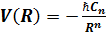, (8.13) где C_n – константа, а n – целое число, зависящее от вида взаимодействия. В квазиклассическом приближении (считаем возмущение адиабатическим, т.е. не приводящим к переходам между состояниями, а траекторию прямолинейной) на атом накладывается внешнее поле

, (8.14) где t = 0 – момент наибольшего сближения, а u – относительная скорость. Сдвиг частоты перехода при этом равен

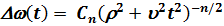, (8.15) где n = 2 для линейного и n = 4 для квадратичного штарк-эффекта.

Предположим сначала, что продолжительность соударения мала по сравнению с временем между соударениями (ударное приближение). Тогда контур линии, излучаемой составной системой “возмущенная частица + излучающий атом”, имеет вид

, (8.16) где сечения, определяющие уширение и сдвиг линии,

,

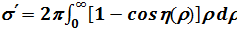зависят от полного сдвига фазы колебаний осциллятора за время столкновения

.

Контур при ударном уширении (8.16), подобно естественному контуру, имеет дисперсионный вид. Выражения для вычисления уширения и сдвига 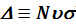для линейного эффекта Штарка (n = 2), резонансного уширения при взаимодействии атомов одного и того же элемента (n = 3), квадратичного эффекта Штарка (n = 4) и уширения Ван-дер-Ваальса (n = 6) приведены, например, в работах [1, 2]. Для оценок естественно считать сильными столкновения, для которых h ~ 1. Это соответствует пролетам с прицельным параметром, меньшим так называемого радиуса Вайскопфа

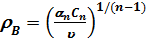, (8.17) где 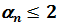(см. [2]). Отсюда частота уширяющих столкновений

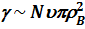. (8.18)

Характерное время столкновения равно 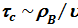, а соответствующая частота W_В = 1 / t_с называется вайскопфовской. Согласно критерия Месси, контур (8.16) правильно описывает форму линии при условии Dwt_с << 1. Центральную часть линии, удовлетворяющую условию Dw << W_В, называют ударной. Ее ширина может превосходить естественную ширину на много порядков. В обратном случае Dwt_с >> 1 атом находится в поле действия других частиц, которое меняется достаточно медленно по сравнению со временем спонтанного излучения. В этом случае справедливо статическое (квазистатическое, статистическое) приближение. Для вычисления контура линии достаточно найти плотность распределения осцилляторов по частотам. Будем считать, что основное поле создает ближайшая частица (приближение ближнего соседа). Вероятность нахождения ближайшей частицы на расстоянии R, R + dR равна

W(R)dR = 4pR²Nexp [- (4p /3) NR³ ] dR = exp [- (R / R₀)³] d (R / R₀), (8.19) где R₀ = (3/4 pN)^1/3. Введя , получаем

. (8.20)

1. Пилюгин Н.Н., Тирский Г.А. Динамика ионизованного излучающего газа. – М.: Изд. МГУ (1989)

2. Собельман И.И. Введение в теорию атомных спектров. – М.: Физматгиз (1963)

Выражение (8.20) имеет смысл только для достаточно больших значений , для которых 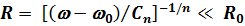, и бинарное приближение справедливо.

Таким образом, центральная часть уширенной линии – лоренцовская, тогда как для больших значений Dw << W_В она описывается статическим контуром. Статическое крыло может располагаться как с длинноволновой, так и с коротковолновой стороны линии в зависимости от направления сдвига термов. В области частот, противоположных по знаку статическому крылу, лоренцовское распределение сменяется экспоненциальным распределением [2, С. 257]. Если бинарное приближение 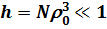становится не справедливым, то пристатическая теория должна учитывать многочастичные взаимодействия. Такая теория была создана Хольцмарком (см. [2]). Распределение Хольцмарка совпадает в асимптотике с выражением (8.20). Однако напомним, что более полно уширение давлением описывает квантовомеханическая теория.

Дата добавления: 2014-01-05