Логическое моделирование вычислительных устройств

Лекция 9. Моделирование устройств на функционально-логическом уровне

Логическое моделирование используется для исследования работоспособности цифровых устройств. Моделирование логических схем - процесс получения временной диаграммы работы устройства. В логическом моделировании оперируют понятиями функциональных моделей элементов, то есть представление элементов в виде " черных ящиков ", для которых связь между входными и выходными сигналами задается в виде булевых уравнений, таблиц истинности или описывается другими способами. Простейшие элементы, составляющие базу данных, используются для описания более сложных устройств.

В зависимости от способа учета времени распространения сигнала методы делятся на синхронный (без учета задержек в элементах схемы) и асинхронный (с учетом задержек). В зависимости от способа представления сигналов - на двоичный и многозначный (троичный, пятизначный и др.); по способу организации работы программы - на метод компиляции и метод интерполяции; по организации очередности моделирования - пошаговый и событийный.

На первом этапе исследуется схема на соответствие заданным функциям без учета задержек сигналов, ограничений элементной базы и внешних условий. Подобная проверка не требует больших затрат машинного времени и позволяет выявить ошибки в структуре устройства, допущенные при его синтезе.

Синхронное двоичное моделирование позволяет проверить соответствие логической схемы системе заданных логических функций без учета задержекв элементах и рисков сбоя.

С инхронные модели функциональных схем

Моделирование синхронных моделей логических схем выполняется методами решения систем логических уравнений, к ним относятся метод простой итерации и метод Зейделя.

Метод простой итерации состоит в том, что уравнение f(x)= 0 заменяем на основе равносильных преобразований уравнением вид x=j(x), а затем строим последовательность приближений к корню уравнения x^*по правилу здесь k -номер итерации. Корень уравнения определяют приближенно с относительной погрешностью , x* -точное решение

Рис. 1.

Для схемы (рис.1) математическая модель есть система следующих логических уравнений

1) e=ac

2)

3)

4) f=bc

5) h=

6)

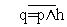
Входные сигналы меняют свое состояние следующим образом a: 0-0, b: 1-0, c: 1-1, d: 0-1.

В таблице 1 представлено ее решение методом простой итерации.

Таблица 1 http://bigor.bmstu.ru/?cnt/?doc=110_Simul/3003.mod/?cou=140_CADedu/CAD.cou

Итерации прекращаются, когда два идущих друг за другом набора сигналов совпадают. Согласно этому методу в уравнения подставляются значения, полученные на предыдущей итерации.

В методе Зейделя в уравнения подставляются значения получения на текущей итерации. В таблице 2 представлено решение этим методом.

Таблица 2

Как видно, число итераций сократилось до четырех. Что бы еще повысить эффективность решения используется предварительное ранжированиеуравнений модели.

Ранжирование заключается в присвоении элементам и переменным модели значений рангов в соответствии со следующими правилами:

1) в схеме разрываются все контуры обратной связи, что приводит к появлению дополнительных входов (псевдовходов);

2) все входные переменные (в том числе и псевдовходы) получают ранг 0;

3) элемент и его выходные переменные получают ранг k, если у элемента все входы проранжированы и старший из них равен k-1.

В соответствии с этим для схемы рис.1 проранжированная последовательность уравнений будет иметь вид:

1) e=ac

2) f=bc

3)

4) h=

5)

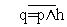
6)

В таблице 3 представлено решение методом Зейделя.

Таблица 3

Таким образом число итераций сократилось до двух.

В основе событийного моделирования лежит обработка процессов только для элементов с изменившимися входными значениями сигналов. Анализ работы цифровых схем показывает, что одновременно в активном состоянии находятся лишь 1 - 10 % всех логических элементов, поэтому событийное моделирование обладает более высоким быстродействием по сравнению со сквозным.

Решение исходной системы уравнений событийным методом представлено в таблице 4.

Таблица 4.

решение прекращается, когда исчезают изменяемые переменные.

Наибольшее распространение получил алгоритм асинхронного событийного моделирования, соединяющий положительные стороны асинхронного и событийного моделирования.

Вторым этапом исследования является проверка работоспособности устройства с учетом задержек элементов, составляющих его структуру, и воздействий различных дестабилизирующих факторов. Этот анализ дает возможность выявить критические состояния сигналов, а так же причины других сбоев. Временное рассогласование входных сигналов элемента может привести к появлению ложного сигнала (сбоя) на выходе логического элемента. Источниками рассогласований являются синусоидальные, трапецеидальные, экспоненциальные сигналы на входе логических элементов, задержки в элементах и линиях передачи.

Можно отметить два основных типа интерпретации понятия " многозначность ": многозначность по виду переключения логических сигналов и многозначность как квантование логического сигнала по уровню.

К первому типу можно отнести такие методы многозначной логики, которые основаны на использовании кроме значений "0" и "1" булевой алгебры различных представлений событийных сигналов:

• при трехзначном моделировании для представления значений величин сигналов берется множество L = {0, 1/2, 1}, где "0" и "1" интерпретируются так же, как и в булевой алгебре, а "1/2" или «Х» обозначает либо переход из одного устойчивого состояния в другое, либо неопределенное состояние.
• четырехзначная модель (алгебра Поста): "0", переходы "0 1" и "1 0", "1";
• пятизначная модель: "0", "0 1", "1 0", "1", "Х" - неопределенное значение;
• восьмизначная модель: "0", "1", чисто алгоритмические переходы "0 1" и "1 0", которые обозначаются специальными символами "+" и "-" соответственно, статические риски сбоя "S0" и "S1", динамические риски сбоя "D+" и "D-";
• девятизначная модель: для моделирования устройств, содержащих микропроцессорные элементы, в сигналах выделяют высокоимпедансное состояние, в которое переходит цепь, когда она отключена от источника питания.

Второй тип многозначности связан с квантованием сигнала по уровню, когда каждой определенной амплитуде сигнала между двумя устойчивыми состояниями логического "0" и "1" присваиваются определенные значения (например, в виде десятичного числа или двоичного кода). Дальнейшая обработка сигналов в системах моделирования сводится к работе с этими значениями. В булевы функции непосредственно вводится дискретная временная функция, а изменения булевых функций во времени оценивается с помощью производной функции по времени. Алгоритм выполнения анализа схем с помощью этого метода достаточно сложен, но позволяет выявлять соотношения задержек в состязающихся цепях, которые определяют наличие или отсутствие сбоя.

Риски сбоев в логических схемах

Под рисками сбоев понимают ситуации, связанные с возможным появлением помех.

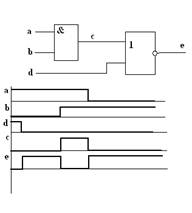
Риски сбоев возникают в ситуациях, когда из-за различных времен задержек сигналов в элементах и линиях связи сигналы на входы элементов приходят неодновременно. В комбинационных схемах это может приводить к появлению ложных сигналов. На рис.1 приведена схема и ее временные диаграммы работы при разновременном приходе сигналов на входы элементов.

Возможность появления помехи на выходе элемента называется статическим риском сбоя (иллюстрируется выходом С, при одновременном приходе сигналов "а" и "b" или при другом соотношении задержек импульса на выходе "с" не было бы).

Возможность многократного переключения элемента из одного состояния в другое вместо правильного однократного называется динамическим риском сбоя (иллюстрируется выходом "е").

 

Дата добавления: 2014-01-05