Определение оптимального ассортимента

Типовые постановки задачи линейного программирования в экономике

Тема 12. Математическое программирование

Вопросы на 5

Прочие виды производственных функций

Функция Кобба-Дугласа. Расчет параметров

???

???

Модель производственной функции. Определение параметров модели. Расчет важнейших показателей деятельности на основе производственной функции. Прогнозирование на основе производственной функции.

1. Постройте систему уравнений МНК для линейной регрессии двух переменных.

1. ???

Раздел 2. Оптимизационные методы прогнозирования

Предполагается, что рассматриваемые методы по большей части уже известны из ранее изученных курсов. Рассматриваются вопросы точности получаемых прогнозов и интерпретации результатов.

Линейное программирование (планирование) – см. курс «Планирование».

Выдержка из – Калихман И.Л. Сборник задач по математическому программированию. – М.:Высшая школа. – 1975г.

Постановка задачи. Имеется р видов ресурсов в количествах b1, … bi, … bn, которые могут быть использованы при производстве q видов изделий. Задана матрица А = || аij ||, где аij, характеризует нормы расхода i-го ресурса на единицу j-го изделия (j = 1, 2,.... q).

Эффективность выпуска единицы j-го изделия характеризуется показателем Сj, удовлетворяющим условию «линейности». Определить план выпуска изделий (оптимальный ассортимент), при кото­ром суммарный показатель эффективности принимает наибольшее значение.

Решение. Обозначив количество единиц j-x изделий, вы­пускаемых предприятием, через Хj >=0, получим математическую модель задачи:

Замечание. Кроме указанных ограничений по ресурсам, в условие задачи, а следовательно, и в ее математическую модель могут вводиться дополнительные ограничения на планируемый выпуск продукции (ограничения по ассортименту, условия комплектности н т. д.).

Пример задачи. Предприятие располагает ресурсами сырья, ра­бочей силой и оборудованием, необходимыми для произ­водства любого из четырех видов производимых товаров. Затраты ресурсов на изготовление единицы данного вида товара, прибыль, получаемая предприятием, а также запасы ресурсов указаны в следующей таблице:

Вид товара Вид ресурса					Объем ресурсов
Сырье, кг
Рабочая сила, ч
Оборудование, станко-ч
Прибыль на единицу товара, руб.

Определить оптимальный ассортимент, максимизирующий товарную продукцию, приняв условие, что продукции №1 должно производится не более 5шт, №2 – не менее 8шт, а №3 и №4 – в отношении 1:2.

12.1.2. ЗАДАЧИ О «СМЕСЯХ»

Постановка задачи. Имеется р ком­понентов (i == 1, 2,..., р), при сочетании которых в раз­личных пропорциях образуются различные смеси. Заданы р чисел Сi характеризующих цену, вес, калорийность и т.д. единицы i-го компонента. Требуется определить состав смеси (т. е. числа X1, …,Xi, … Xp), для которой суммарная характеристика (цена, вес и т. д.) окажется наи­лучшей.

При этом предполагается, что в состав каждого компонента входят q веществ. Для каждого вещества задано число Bj, указывающее минимально необходимое содержание j-го вещества в смеси. Через Aij обозначено количество j-го вещества (j = 1, 2,..., q), которое входит в состав единицы i-го компонента.

Решенне. Предпо­лагается, что количество вещества в смеси равно сумме количеств вещества в каждой из компонент смеси, т. е. если смесь состоит из X1 единиц 1-го компонента, X2 единиц 2-го компонента и т. д., то количество вещества j в смеси равно . Из условия обязательного минимального содержания каждого из веществ в смеси получим си­стему неравенств:

Кроме того, очевидно, что

Наконец, суммарная характеристика смеси выразится равенством .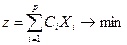

Замечания.1. Кроме ограничений, по содержанию отдельных веществ в смеси, в задаче могут фигурировать ограничения по имеющимся запасам отдельных компонентов или по предельным нормам их включения в смеси. Могут задаваться также пропорции, в которых некоторые из компонентов должны входить в состав смеси.

2. Если известны условия изготовления компонентов с учетом имеющихся для этой цели ресурсов, то возникает более сложная объединенная задача составления оптимальной смеси, для которой будут с наибольшим эффектом использованы ресурсы в производстве компонентов. Так, например, при составлении рациона кормления можно определить оптимальную структуру посевов, обеспечивающих кормление имеющегося поголовья скота наилучшим образом.

Ресурсами в данном случае служат участки земли, на которых выращиваются различные компоненты, включаемые в рацион.

Пример задачи. Нефтеперерабатывающий завод получает 4 полуфабриката: 400 тыс. л алкилата, 250 тыс. л крекинг-бензина, 350 тыс. л бензина прямой перегонки и 100 тыс. л. изопенттона. В результате смешивания этих четырех компонентов в разных пропорциях образуются три сорта авиационног бензина: бензин А— 2:3:5:2, бензин В — 3: 1: 2: 1 и бензин С — 2: 2: 1: 3.

Стоимость 1 тыс. л указанных сортов бензина характеризуется числами: 120 руб., 100 руб. и 150 руб.

Определить план смешения компонентов, при котором будет достигнута максимальная стоимость всей продукции. (Вариант: Определить оптимальный план смешения из усло­вия максимального использования компонентов.)

12.1.3. ЗАДАЧИ О «РАСКРОЕ»

Постановка задачи. На раскрой (распил, обработку) поступает s различных материалов. Требуется изготовить из них q различных изделий в коли­честве, пропорциональном числам B1, B2, …, Bk, …,Bq.

Каждая единица j-го материала (j == 1,2,..., s) может быть раскроена р различными способами, причем исполь­зование i-ro способа (i == 1,..., р) дает единиц k-x из­делий.

Найти план распила, обеспечивающий максимальное число комплектов, если материалов j-го вида поступает Dj единиц.

Решение. Обозначим через Xij количество единиц j-го материала, раскраиваемых по i-му способу (всего таких переменных будет p*s). Переменные Xij, очевидно, должны удовлетворять ограничениям:

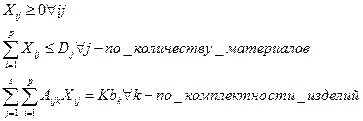где K — число комплектов изготавливаемых изделий.

Задача заключается в максимизации Z == K при вышеуказанных условиях.

В частном случае, когда на обработку поступает материал только одного образца (т. е. s = 1), в количестве D ед., модель принимает более простой вид:

Пример задачи. Для изготовления брусьев трех размеров: 0,6м, 1,5м и 2,5м в соотношении 2: 1: 3 на распил поступают бревна длиной в 3 м. Определить план распила, обеспечивающий максимальное число комплектов.

Решение. Прежде всего, определим всевозможные способы распила бревен, указав, сколько соответствующих брусьев при этом получается.

Способы распила (i)	Получаемые брусья	Количества бре­вен, распилен­ных по i-му способу
0,6	1,5	2,5
		—	—	X1
			—	X2
	—		—	X3
	—	—		X4
Комплект

Теперь составляем математическую модель, приняв, что всего поступает на распил D бревен: максимизировать число комплектов Z=K при условиях, что все бревна должны быть распилены (X1+X2+X3+X4=D) и что число брусьев каждого размера должно удовлетворять условию комплектности:

5Х1+2Х2=2К; Х2+2Х3=1К; Х4=3К.

Из последнего равенства, определив К=1/3Х4, и исключив К из остальных выражений, придем окончательно к следующей задаче:

После решения ее получим оптимальное решение задачи Х={4/39, 5/39, 0, 10/13} н Z=10/39.

Таким образом, 10,2% (4/39) общего числа поступающих бревен следует распиливать по 1-му способу, 12,8% — по 2-му способу и 77% — 4-му способу; 3-й способ распила применять не следует. При этом будет произведено 10/39 комплекта на каждые D брёвен.

Дата добавления: 2014-01-05