Визначення натурального числа і нуля

Означення. Натуральні числа – це числа, які застосовують при лічбі предметів. Натуральні числа є порядкові і кількісні.

Вказуючи при лічбі на кожен елемент деякої множини, називають порядкові натуральні числа (перший, другий і т. д.). Наприклад: перелічуючи елементи множини 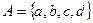називаємо слова «перший», «другий», «третій», «четвертий», тобто використали порядкові натуральні числа. Перелічивши елементи множини, вони дають кількісну характеристику цієї множини. У нашому прикладі ми говоримо, що їх у множині А «чотири», тобто даємо кількісну характеристику множини А і використовуємо при цьому кількісне натуральне число. Іншими словами, ми використали множину чисел , яку називають відрізком натурального ряду.

Означення. Відрізком натурального ряду називається множина натуральних чисел, яка не перевищує натурального числа а. Позначається N_а. Будь-який відрізок N_а при а >1 містить 1.

Наприклад: N₄ є множина натуральних чисел 1, 2, 3, 4; тобто N₄ = .

Лічба елементів множини А – це встановлення взаємнооднозначної відповідності між елементами множини А і відрізком натурального ряду чисел N_а.

Число а називають числом елементів у множині А. Позначається: п (А)=а. Це число для даної множини єдине і є кількісним натуральним числом. Отже, при перелічуванні елементів множини використовуються порядкові натуральні числа, які виражаються числівниками «перший», «другий», «третій» і т. д. (тобто відповідають на питання, який при лічбі); для встановлення кількості елементів множини (тобто для відповіді на питання «скільки»), використовуються кількісні натуральні числа, які виражаються числівниками «один», «два», «три» і т.д.

Таким чином, кількісні і порядкові натуральні числа знаходяться в тісному взаємозв’язку. Тісний зв’язок порядкового і кількісного натурального чисел знайшов своє відображення в початковому навчанні математики. Так при вивченні чисел першого десятка відповідь на питання: «Скільки предметів в даній групі?» - дається кількісним натуральним числом, а на питання: «Який при лічбі буде даний предмет?» - відповідь дається порядковим натуральним числом.

При лічбі дотримуються певних правил:

1. першим при лічбі може бути вказаним будь - який елемент множини;

2. жоден елемент множини не повинен бути пропущеним;

3. не можна лічити двічі один і той же елемент множини;

4. останнє назване число вказує на кількість елементів множини.

3. Теоретико – множинний зміст кількісного натурального числа і нуля.

Розкриємо зміст кількісного натурального числа з теоретико-множинних позицій, використовуючи поняття рівнопотужних множин.

Відберемо в один клас всі скінчені множини, які рівно потужні деякій скінченій множині А; в другий клас множини, рівно потужні іншій скінченій множині - В і т. д. В силу того, що відношення рівно потужності є відношенням еквівалентності, всі скінченні множини будуть розподіленні за класами еквівалентності. Всі множини одного класу мають спільну властивість, а саме - в них однакова потужність (тобто однакова кількість елементів - що і є кількісним натуральним числом).

Означення. Кількісним натуральним числом називається загальна властивість класу скінченних рівнопотужних множин.

Кожному класу відповідає одне і тільки одне натуральне число.

Кожному натуральному числу відповідає тільки один клас рівнопотужних множин.

Кожній скінченій множині відповідає одне і тільки одне натуральне число а = n (А), але кожному натуральному числу відповідають різні скінчені множини одного класу еквівалентності.

Наприклад: числу 3 відповідають множина сторін трикутника, множина його вершин, множина кутів, множина букв у слові «мир» і т. д.

Теоретико-множинний смисл числа нуль: „Нуль - це загальна властивість класу порожніх множин: 0 = п (Ø)”.

В початковому курсі математики при розкритті поняття числа в темі: «Числа першого десятка» кількісне натуральне число розглядається як загальна властивість класу скінчених рівнопотужних множин.

4. Властивості множини цілих невід’ємних чисел.

1. Множина цілих невід’ємних чисел впорядкована. Наприклад, вона впорядковується відношенням «менше», яке є транзитивним і антисиметричним.

Для будь - яких цілих невід’ємних чисел а і b може виконуватись одне з трьох відношень: а < b, а = b, а > b.

Можна розташувати числа так, щоб для будь-яких двох чисел спочатку йшло число менше, тоді отримаємо ряд цілих невід’ємних чисел: 0, 1, 2, З, 4,...

2. Множина цілих невід’ємних чисел нескінчена. Для кожного цілого невід’ємного числа а можна вказати число, яке слідує безпосередньо за ним. Це число а + 1.

3. Множина цілих невід’ємних чисел дискретна. Це означає, що не можна вказати таке натуральне число, яке знаходиться між цілими невід’ємних числами а і а + 1. Самі ці числа називаються сусідніми.

При вивченні чисел першого десятка в 1 класі з’ясовується утворення кожного числа натурального ряду (прилічуванням і відлічуванням одиниці). При цьому використовуються поняття «слідує», «передує», «попереднє число», «наступне число», тобто створюються умови, щоб учні зрозуміли властивості чисел натурального ряду:

• будь-яке число натурального ряду може бути отримане додаванням одиниці до того числа, яке при лічбі називається перед ним;
• будь-яке число натурального ряду на 1 більше, ніж попереднє.

Дата добавления: 2014-01-05