Еластичність функції

Еластичність

ЧИСЛЕННЯ В ЕКОНОМІЧНОМУ АНАЛІЗІ

ЗАСТОСУВАННЯ МЕТОДІВ ДИФЕРЕНЦІАЛЬНОГО

Важливим напрямом застосування диференціального числення в економіці є введення з його допомогою поняття еластичності. Коефіцієнт еластичності показує відносну зміну досліджуваного економічного показника внаслідок одиничної відносної зміни економічного фактора, від якого він залежить, за незмінності інших факторів, що впливають на нього.

Нехай задано функцію y = f (x). Зміна незалежної змінної x на ∆x зумовлює зміну функції y на ∆y. Виникає запитання: як суттєво змінюється функція y залежно від зміни аргументу x? Одним із показників реагування однієї змінної на зміну іншої змінної є похідна 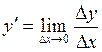, що характеризує швидкість зміни функції внаслідок зміни аргументу. Але в економіці цей показник незручний тим, що він залежить від вибору одиниць величин.

Наприклад, розглянувши функцію попиту на цукор q від його ціни p (q = q (p)), побачимо, що значення похідної 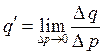за кожної ціни p, яка виражається в гривнях, залежить від того, в чому виражається попит на цукор – у кілограмах або тоннах. У першому випадкові похідна виражається в кілограмах на гривню, в другому – в тоннах на гривню, й відповідно її значення, за однієї й тієї самої ціни, будуть різними залежно від одиниці попиту. Тому для якісного визначення зміни функції відносно зміни аргументу в економіці вивчають зв’язок не абсолютних змін величин x і y(∆x i ∆y), а їхніх відносних або процентних змін.

Означення Еластичністю функції y = f (x) називають границю відношення відносного приросту функції y до відносного приросту аргументу x при ∆ x → 0 і позначають

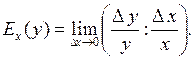(1)

Еластичність функції наближено виражає, на скільки процентів зміниться функція y = f (x) у разі зміни незалежної змінної x на 1 %, тобто

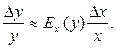
З означень еластичності й похідної випливає, що

або

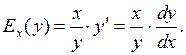(2)

Оскільки для функції y = f (x) маємо 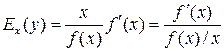, то еластичність виражає відношення граничного значення f ' (x) до середнього значення функції f (x) / x у точці x.

Враховуючи, що 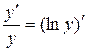і 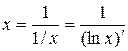, дістаємо

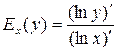, (3)

тобто еластичність можна подати у вигляді «логарифмічної» похідної.

Як і похідна, еластичність має простий геометричний зміст: Оскільки y' = tg α, де α – кут нахилу дотичної, проведеної до графіка функції y = f (x) у точці x, то за означенням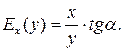

Знайдемо еластичність функції в довільній точці C (x; y). Для цього проведемо дотичну АВ до графіка функції y = f (x) у точці С. Нехай А і В – точки перетину дотичної з осями О x і О y відповідно.

Розглянемо спадну опуклу вниз функцію y = f (x). (рис. 1)

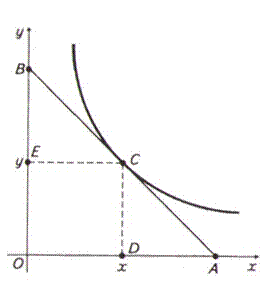
рис. 1

З трикутника ACD дістанемо

,

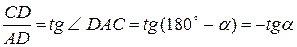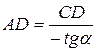, CD = f (x),

Тобто 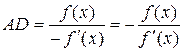. Із подібності трикутників CBE та ACD випливає, що 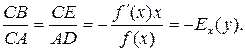Таким чином,

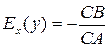, (4)

Тобто геометрично еластичність спадної функції дорівнює відношенню відстаней по дотичній від точки С до її перетину з осями Oy і Ox, взятому зі знаком «–». У випадку зростаючої функції, опуклої вниз (рис. 2) і опуклої вгору (рис. 3), еластичність функції також дорівнюватиме відношенню CB / CA, а знак еластичності визначатиметься напрямом відрізків CB і CA. Якщо точки A і В лежать по один бік від точки С на дотичній (як на рис. 2 і 3), то у формулі (4) треба брати знак «+». Якщо точки A і В лежать по різні боки від точки С (див. рис. 7.1), то у формулі (7.4) треба брати знак «–».

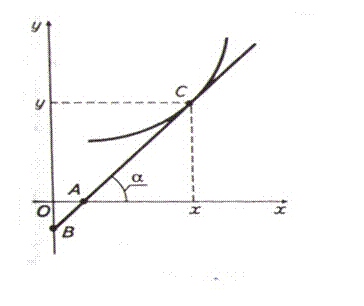
рис. 2

рис. 3

Отже, еластичність функції (за абсолютним значенням) дорівнює відношенню відстаней по дотичній від даної точки графіка функції до точок її перетину з осями Ох і Оу.

Означення. Якщо │ E_x (y)│ < 1, то функцію називають нееластичною (її відносний приріст спадає).Якщо │ E_x (y)│ > 1, то функцію називають еластичною (її відносний приріст зростає).

Зауваження. Еластичність функції, зображеної на рис. 2, більша за одиницю (оскільки CB > CA), а на рис. 3 – менша від одиниці (оскільки CB < CA).

Дата добавления: 2014-01-05