Создание приложений для решения типовых задач аналитической геометрии

Лекция № 6

Рассмотрим ряд задач аналитической геометрии и правило их набора в среде Matlab.

Задача 1.

Даны три точки М₁(х₁; у₁), М₂(х₂; у₂), М₃(х₃; у₃), уравнение линии Г₁ и прямые L₁; L₂

Требуется:

1. Проверить (графически и аналитически), лежит ли точка М₁ на линии Г₁.

2. Найти расстояние между точками М₂ и М₃.

3. разделить отрезок М₁М₂ точкой С пополам и отрезок М₁М₃ точкой Д в заданном отношении λ=2.

4. Преобразовать уравнение прямой L₁ в уравнение:

а) с угловым коэффициентом;

б) в отрезках на осях.

5. Составить уравнение прямой L₃, параллельной прямой L₂ и проходящей через точку М₂.

6. Найти уравнение прямой L₄, проходящей через точки М₁, М₂.

7. Определить расстояние от точки М₁ до прямой L₂.

8. Найти точку пересечения прямых L₁ и L₂ и угол между ними.

9. Построить прямые L₁, L₂, линию Г₁ на одном графике, разными цветами и разными стилями.

Решение.

1. Для того чтобы проверить графически лежит ли точка на линии, необходимо:

Задать координаты данной точки. Ввести диапазон для аргумента х и уравнение кривой и с помощью функции plot построить точку и кривую на одном графике.

Для проверки аналитически в математике необходимо координаты точки подставить в соответствующее уравнение кривой и получить верное тождество. В Matlab.нужно вести координаты данной точки и уравнение кривой при этом вместо переменной х подставить координату точки. И если получиться вторая координата точки то можно сделать вывод, что точка лежит на кривой, в противном случае - нет.

1) М₁(-4; 13), М₂(-12; 2), М₃(-3; 0); Г₁: х²-у²-4х=0; L₁: 2х+2у-3=0; L₂: 3х+у+2=0;

1. графически:

>> x=-10:0.1:14;

>> y1=sqrt(-4.*x+x.^2);

>> x3=-4; y3=13;

>> y2=-sqrt(-4.*x+x.^2);

>> plot(x,y1,x,y2,x3,y3,'*')

аналитически:

>> x3=-4; y3=13;

>> y3=sqrt(-4.*x3+x3.^2)

y3 =

>> x3=4; y3=3;

>> y3=-sqrt(4.*x3-x3.^2)

y3 =

2. Расстояние между точками находится по формуле . В Matlab

>> x1=-2; y1=2;

>> x2=3; y2=0;

>> d=sqrt((x2-x1)^2+(y2-y1)^2)

3. Деление отрезка пополам: ;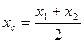

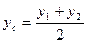
>> M1=[-4 13];

>> M2=[-12 2];

>> C=(M1+M2)./2

Деление отрезка в заданном отношении ,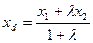

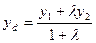
>> D=(M1+l.*M2)./(1+l)

4. Преобразование уравнения прямой:

а) с угловым коэффициентом: у=кх+b1

в) в отрезках на осях:

а) у=кх+b1

>> a=2;b=2;c=-3;

>> k=-a/b; b1=-c/b;

>> [k,b1

в)

>> a=2;b=2;c=-3;

>> a1=-c/a; b1=-c/b;

>> [a1,b1]

5. Уравнение прямой параллельной данной и проходящей через заданную точку: 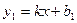, . Коэффициенты к одинаковы, а потом в полученное уравнение подставляем координаты точки и находим b.

>> a=3;b=-1;

>> x2=-2;y2=2;

>> [-b,a,(b*x2-a*y2)]

6. Найти уравнение прямой L₄, проходящей через точки М₁, М₂.

Пусть ,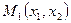

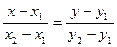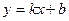Тогда уравнение искомой прямой имеет вид: или , где ,

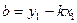
>> x1=4; y1=3;

>> x2=-2;y2=2;

>> k=(y2-y1)/(x2-x1); b=y1-x1*((y2-y1)/(x2-x1));

>> [k,b]

7. Определить расстояние от точки М₁ до прямой _.: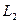

Пусть прямая имеет уравнение: 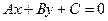. Тогда расстояние от точки до прямой определяется по формуле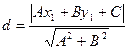

>> A=3;B=-1;C=2;

>> x1=4;y1=3;

>> d=(abs(A*x1+B*y1+C))/sqrt(A^2+B^2)

8. Найти точку пересечения прямых L₁ и L₂ и угол между ними.

Чтобы найти точку пересечения прямых, в математике, надо решить систему из уравнений данных прямых. В Matlab система решается с помощью функции solve

>> syms x,y;

Y=solve('2*x+y=3', '-3*x+y=2')

Y =

x: [1x1 sym]

y: [1x1 sym]

>> Y.x

>> Y.y

Угол между прямыми вычисляется по формуле:

Дополнительные формулы:

1. площадь треугольника:Каковы бы ни были три точки 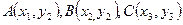площадь треугольника задается формулой

2. Если прямая задана уравнением вида: 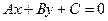, то

3. Уравнение окружности: , где 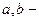координаты центра, радиус окружности.

4. Каноническое уравнение эллипса: , если , то большая ось эллипса лежит на оси 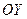, уравнение связи: , эксцентриситет:или 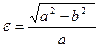, фокальные радиусы: , , 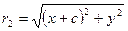уравнение директрис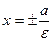

При построении эллипса и окружности лучше канонические уравнения сводить к параметрическому виду: окружность , эллипса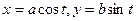

5. Каноническое уравнение гиперболы: 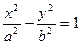, , 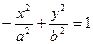уравнение связи: , уравнения асимптот: , эксцентриситет:или 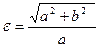, отношение -это тангенс угла наклона асимптоты к си 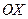, уравнение директрис 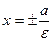. При построении гиперболы необходимо строить две ветви гиперболы, а именно .

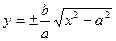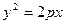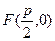6. Каноническое уравнение параболы: ,, уравнение директрисы , координаты фокуса . При построении параболы необходимо строить две полуветви параболы, а именно

7. Полярное уравнение эллипса, гиперболы, параболы: , где для параболы фокальный параметр ее параметр, для эллипса и гиперболы 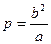,.если 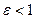, то уравнение определяет эллипс, если , то гиперболу, и если 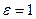,то параболу.

Дата добавления: 2014-01-05