Погрешность вычислений

Пусть A и а — два «близких» числа; условимся считать A — точным, а — приближенным.

Определение 1. Абсолютная и относительная погрешность.

Величина Δa = |A – а| называется абсолютной погрешностью приближенного числа а, а его относительной погрешностью. Числа Δ_a и δ_a такие, что D_a³Da и 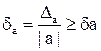, называются оценками или границами абсолютной и относительной погрешностей соответственно (к Δ_a и δ_a часто применяют также термин «предельные погрешности»).

Так как обычно истинные погрешности не известны, то там, где не может возникнуть недоразумений, будем иногда называть Δ_a и δ_a просто абсолютной и относительной погрешностями.

Определение 2. Значащие цифры.

Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой слева.

Пример 1. Значащие цифры.

У чисел a = 0,0 3045, а = 0,0 3045000 значащими цифрами являются подчеркнутые цифры. Число значащих цифр в первом случае равно 4, во втором — 7.

Определение 3. Верная цифра.

Значащую цифру называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.

Пример 2. Верная цифра.

а = 0,0 3045, Δa = 0,000003; а = 0,0 30450 00, Δa = 0,0000007; подчеркнутые цифры являются верными.

Определение 4. Все верные цифры.

Если все значащие цифры верные, то говорят, что число записано со всеми верными цифрами.

Пример 3. Все верные цифры.

При a = 0,03045, Δa = 0,000003 число a записано со всеми верными цифрами.

Поставим вопрос о грубом оценивании погрешности результата вычисления значения дифференцируемой функции u = f(x₁, x₂, …, x_n) приближенных аргументов x₁, x₂, …, x_n, если известны границы их абсолютных погрешностей , , …, , 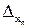соответственно. В этом случае точные значения аргументов 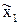, , …, 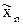лежат соответственно на отрезках 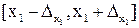, , 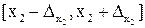…, , а точная абсолютная погрешность результата u = f(x₁, x₂, …, x_n) есть

—

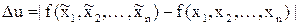модуль полного приращения функции. Главной, т.е. линейной частью этого приращения является, как известно, полный дифференциал du. Таким образом, имеем:

,

т.е. за границу абсолютной погрешности результата приближенно может быть принята величина

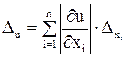. (1)

Отсюда легко получается формула приближенной оценки относительной погрешности значения u:

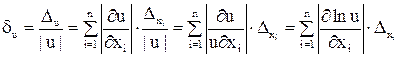. (2)

Как частные случаи формул (1), (2) (точных для функций, линейных относительно x_i или ln x_i соответственно) можно получить известные правила оценивания погрешностей результатов арифметических действий.

Действительно, пусть u = ± x₁ ± x₂ ± … ± x_n. Тогда 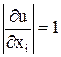и 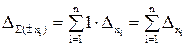, т.е. при сложении и вычитании приближенных чисел их предельные абсолютные погрешности складываются.

Пусть теперь u = x₁ × x₂ × … × x_n, где можно считать все сомножители положительными. Так как ln u = ln x₁ + ln x₂ + … + ln x_n и , то, согласно (2),

(3)

Если же , где x₁, x₂ > 0, то ln u = ln x₁ – ln x₂, и, значит,

Последнее вместе с (3) означает известный результат о сложении предельных относительных погрешностей при умножении и делении приближенных чисел.

Возвращаясь к сложению, рассмотрим относительную погрешность суммы n положительных приближенных чисел x₁, x₂, …, x_n, имеющих границы относительных погрешностей 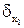, , …, 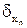соответственно:

,

где . Полученное неравенство говорит о том, что относительная погрешность суммы n положительных приближенных чисел не превосходит максимальной относительной погрешности слагаемых.

С вычитанием приближенных чисел дело обстоит хуже: оценка

относительной погрешности разности x₁ – x₂ двух приближенных положительных чисел указывает на возможность сильного возрастания погрешности при x₁ – x₂ ® 0. В этом случае говорят о потере точности при вычитании близких чисел.

Часто возникает обратная задача теории погрешностей: какой точности данные нужно подать на вход, чтобы на выходе получить результат заданной точности? Применительно к поставленной выше прямой задаче оценивания погрешности результата вычисления значения функции при заданных оценках погрешностей аргументов обратная задача заключается в оценивании величин Δx_i (или dx_i) по известной величине Δu. Для случая дифференцируемой функции одной переменной грубое решение обратной задачи тривиально: если y = f(x), то

Δy» |dy| = |f'(x)|Δx, откуда 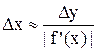. Для функции большего числа переменных обратная задача, вообще говоря, некорректна. Нужны дополнительные условия. Например, применяют принцип равных влияний, состоящий в предположении, что частные дифференциалы 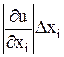в (1) одинаково влияют на погрешность значения функции; тогда

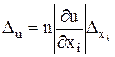, откуда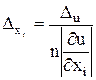

В качестве другого довольно естественного допущения можно принять равенство относительных погрешностей всех аргументов, т.е. считать 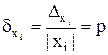при всех i = 1, 2,..., n. Тогда 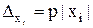и, значит, . Из последнего равенства получаем величину 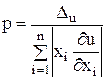(характеризующую относительный уровень точности задания аргументов), на основе которой за границы абсолютных погрешностей аргументов принимаем . Имеются и другие, более сложные подходы к решению обратной задачи.

Статистический и технический подходы к учету погрешностей действий

Рассмотренный выше аналитический (или классический) способ учета погрешностей действий, предполагающий точное оценивание погрешностей, основанное либо на приведенных в предыдущем параграфе правилах подсчета погрешностей арифметических действий, либо на параллельной работе с верхними и нижними границами исходных данных, имеет два существенных недостатка. Во-первых, этот способ чрезвычайно громоздок и не может быть рекомендован при массовых вычислениях. Во-вторых, он учитывает крайние, наихудшие случаи взаимодействия погрешностей, которые допустимы, но маловероятны. Ясно, что, например, при суммировании нескольких приближенных чисел (полученных в результате измерений, округлений или каким-либо другим путем) среди них почти наверное будут слагаемые как с избытком, так и с недостатком, т.е. произойдет частичная компенсация погрешностей. При больших количествах однотипных вычислений вступают в силу уже вероятностные или статистические законы формирования погрешностей результатов действий. Например, методами теории вероятностей показывается, что математическое ожидание абсолютной погрешности суммы n слагаемых с одинаковым уровнем абсолютных погрешностей, при достаточно большом n, пропорционально . В частности, если n > 10 и все слагаемые округлены до m-го десятичного разряда, то для подсчета абсолютной погрешности суммы S применяют правило Чеботарева

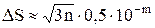(4)

Различие в результатах классического и статистического подходов к оцениванию погрешности суммы рассмотрим на примере оценки погрешности среднего арифметического нескольких приближенных чисел.

Пример 4. Погрешность среднего арифметического.

Пусть — среднее арифметическое n (n > 10) приближенных чисел (например, результатов измерений), имеющих одинаковый уровень абсолютных погрешностей . Тогда классическая оценка абсолютной погрешности величины x есть

,

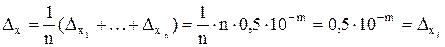т.е. такая же, как и у исходных данных. В то же время по формуле (4) имеем

.

Как видим, применение правила Чеботарева приводит к естественному выводу о том, что арифметическое усреднение результатов измерений или наблюдений увеличивает точность, чего нельзя сказать на основе классической теории погрешностей.

Прямое применение вероятностно-статистических оценок погрешностей также является достаточно сложным делом и вряд ли может быть рекомендовано при рядовых массовых вычислениях. Однако именно такие оценки подкрепляют практические правила работы с приближенными числами, составляющие основу так называемого технического подхода. Этот подход связывают с именем известного русского кораблестроителя, математика и механика академика А. Н. Крылова. Согласно принципу А. Н. Крылова, приближенное число должно записываться так, чтобы в нем все значащие цифры, кроме последней, были верными и лишь последняя была бы сомнительна, и притом в среднем не более чем на одну единицу. Напомним, что значащими цифрами числа в его позиционной записи называются все его цифры, начиная с первой ненулевой слева. Значащую цифру приближенного числа называют верной, если абсолютная погрешность числа не превосходит единицы разряда, в котором стоит эта цифра (или половины единицы; в этом случае иногда применяется термин верная в узком смысле).

Чтобы результаты арифметических действий, совершаемых над приближенными числами, записанными в соответствии с принципом А. Н. Крылова, также соответствовали этому принципу, нужно придерживаться следующих простых правил:

1) при сложении и вычитании приближенных чисел в результате следует сохранять столько десятичных знаков, сколько их в приближенном данном с наименьшим количеством десятичных знаков;

2) при умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближенное данное с наименьшим числом значащих цифр;

3) результаты промежуточных вычислений должны иметь один-два запасных знака (которые затем должны быть отброшены).

Таким образом, при техническом подходе к учету погрешностей приближенных вычислений предполагается, что в самой записи приближенного числа содержится информация о его точности. И хотя прямая выгода от применения приведенных правил работы с приближенными числами может быть получена лишь при ручном счете (не нужно оперировать с цифрами, не влияющими на информативную часть приближенного результата), их знание и понимание помогает правильной интерпретации компьютерных расчетов, а иногда и самой организации таковых.

Дата добавления: 2014-01-05