
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Знакопеременные ряды. Абсолютная и условная сходимость
|
|
|
|
Знакочередующиеся ряды. Признак Лейбница.
Рассмотрим ряды с членами, имеющими любой знак. Прежде всего остановимся на знакочередующихся рядах. В таких рядах слагаемые с положительными и отрицательными знаками чередуются между собой:
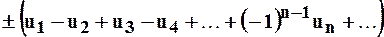 (*)
(*)
Где 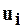 – положительные числа.
– положительные числа.
Теорема 4(Признак Лейбница): Если в знакочередующемся ряде (*) абсолютные величины членов ряда убывают, начиная с некоторого номера, т.е. имеем: 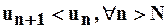 и общий член ряда по абсолютной величине стремится к нулю:
и общий член ряда по абсолютной величине стремится к нулю: 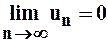 , то ряд (*) сходится, причём его сумма (по абсолютной величине) меньше, чем абсолютная величина его первого члена и остаток ряда меньше абсолютной величины первого из отбрасываемых слагаемых, т.е.
, то ряд (*) сходится, причём его сумма (по абсолютной величине) меньше, чем абсолютная величина его первого члена и остаток ряда меньше абсолютной величины первого из отбрасываемых слагаемых, т.е.  .
.
Доказательство:
Для определённости в качестве ряда (*) рассмотрим ряд:

Представим сумму первых «2n» слагаемых ряда и частичную сумму  :
: 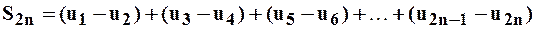
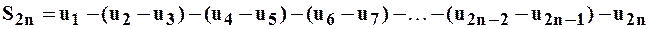
Причём, каждая разность в скобках положительна по условию (т.к. 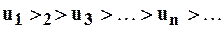 ) поэтому из первого представления чётной суммы
) поэтому из первого представления чётной суммы  видно, что эта величина положительная и возрастает с ростом
видно, что эта величина положительная и возрастает с ростом 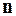 . Из второго представления суммы следует:
. Из второго представления суммы следует:  .
.
Положительные величины  возрастают с ростом
возрастают с ростом 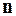 , оставаясь всё время меньше
, оставаясь всё время меньше  , а значит, по признаку Вейерштрасса эти величины стремятся к некоторому пределу:
, а значит, по признаку Вейерштрасса эти величины стремятся к некоторому пределу: 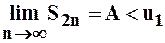 .
.
Для нечётных частичных сумм рассмотрим равенство:  , в котором
, в котором 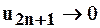 при
при 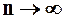 . Откуда следует:
. Откуда следует: 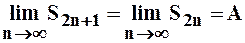 . Это означает, что исходный ряд сходится. Докажем вторую часть утверждения теоремы, т.е.
. Это означает, что исходный ряд сходится. Докажем вторую часть утверждения теоремы, т.е. 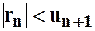 . Для этого представим ряд в виде:
. Для этого представим ряд в виде:  , где
, где 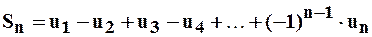 – частичная сумма ряда. Заметим, что остаток ряда представляет также знакочередующийся ряд и его первый член есть
– частичная сумма ряда. Заметим, что остаток ряда представляет также знакочередующийся ряд и его первый член есть  , а потому, его сумма по абсолютной величине меньше, чем его первое слагаемое: т.е.
, а потому, его сумма по абсолютной величине меньше, чем его первое слагаемое: т.е. 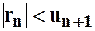 .
.
Замечание 1. Признак Лейбница позволяет в случаях, когда применима теорема Лейбница, не только установить сходимость знакочередующегося ряда, но и оценить ошибку, допускаемую при замене ряда конечной суммой (отбрасывание всех членов ряда, начиная с некоторого номера 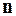 ).
).
Пример 1. По теореме Лейбница сразу видно, что знакочередующийся ряд:

 сходится, т.к. выполнены требования теоремы, т.е.
сходится, т.к. выполнены требования теоремы, т.е. 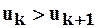 и
и  . Пусть сумма этого ряда равна
. Пусть сумма этого ряда равна 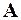 . Причём
. Причём  . С другой стороны:
. С другой стороны:  , причём
, причём  , т.е. если вместо полного ряда будем рассматривать только его часть, то допускается ошибка, меньшая чем
, т.е. если вместо полного ряда будем рассматривать только его часть, то допускается ошибка, меньшая чем 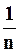 .
.
1.4. Абсолютная и условная сходимость.
Рассмотрим ряд:  , (1)
, (1)
членами которого являются действительные числа (как положительные так и отрицательные). Одновременно с рядом (1) рассмотрим ряд, составленный из абсолютных величин:
 (2)
(2)
Теорема 5: (Достаточный признак сходимости)
Если ряд, составленный из абсолютных величин (2) сходится, то исходный ряд (1) также сходится.
Доказательство:
Обозначим через 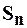 – частичную сумму
– частичную сумму 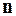 – первых членов ряда (1).
– первых членов ряда (1).
Пусть  – есть сумма всех положительных членов из
– есть сумма всех положительных членов из 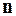 первых членов ряда (1),
первых членов ряда (1),
 – есть сумма всех отрицательных членов из
– есть сумма всех отрицательных членов из 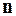 первых членов ряда (1).
первых членов ряда (1).
Тогда: 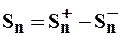 и
и 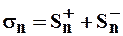 , где
, где  – частичная сумма ряда (2).
– частичная сумма ряда (2).
Так как по условию теоремы ряд (2) сходится, т.е. 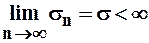 , а
, а  ,
,  – есть положительные и возрастающие функции, зависящие от
– есть положительные и возрастающие функции, зависящие от 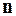 , причём:
, причём:
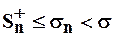 , т.к.
, т.к.  – это часть
– это часть  и
и 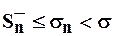 по этой же причине, тогда, по признаку Вейерштрасса они имеют пределы, не превосходящие
по этой же причине, тогда, по признаку Вейерштрасса они имеют пределы, не превосходящие  . Вследствие этого:
. Вследствие этого:
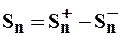 также имеет конечный предел, т.е. ряд (1) – сходится.
также имеет конечный предел, т.е. ряд (1) – сходится. 
Замечание1: Этот достаточный признак не является необходимым, т.е. ряд  может сходится и тогда, когда ряд
может сходится и тогда, когда ряд 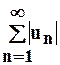 – расходится.
– расходится.
Пример 2. Ряд  – сходится, тогда как гармонический ряд
– сходится, тогда как гармонический ряд  расходится.
расходится.
¨ Ряд, абсолютные величины членов которого образуют сходящийся ряд, называется абсолютно сходящимся.
¨ Если ряд сходится, а ряд, образованный из абсолютных величин его членов расходится, то данный ряд называется не абсолютно или условно сходящимся.
Замечание 2: Абсолютно сходящиеся ряды обладают переместительным свойством.
В ряде не абсолютно сходящемся нельзя переставлять члены местами, т.к. от этого может измениться сумма всего ряда.
Пример 3. Рассмотрим знакочередующийся ряд:
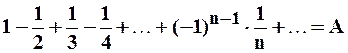 , переставим у него члены так, чтобы за всяким положительным его членом следовали два ближайших отрицательных члена:
, переставим у него члены так, чтобы за всяким положительным его членом следовали два ближайших отрицательных члена:
 и т.д. Легко видеть, что сумма нового ряда будет равна
и т.д. Легко видеть, что сумма нового ряда будет равна  , а именно (складывая соседние положительные и отрицательные члены):
, а именно (складывая соседние положительные и отрицательные члены): 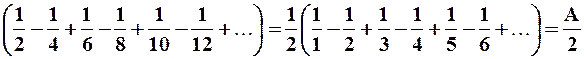 .
.
Таким образом, переставив члены знакочередующегося ряда получили различные суммы.
Замечание 3: Абсолютно сходящиеся ряды обладают свойством перемножения. Под произведением двух сходящихся рядов:
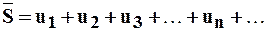 (3)
(3)
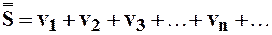 (4)
(4)
понимают ряд, образованный из всевозможных парных произведений членов данных рядов, расположенных в следующем порядке:
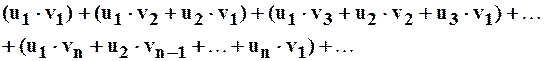 (5)
(5)
В каждой группе членов этого ряда, объединённых в скобки, сумма индексов сомножителей постоянна. На первом месте она равна 2, на втором – 3, и т.д.
Теорема 6: (без доказательства) Если ряды (3) и (4) абсолютно сходятся, то их произведение есть также абсолютно сходящийся ряд, сумма которого равна произведению сумм сомножителей (исходных рядов):  .
.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 623; Нарушение авторских прав?; Мы поможем в написании вашей работы!