Количество информации, получаемой в сообщении

До сих пор формулы приводились для расчета энтропии (неопределенности) H с указанием на то, что H в них можно заменять на I, потому что количество информации, получаемое при полном снятии неопределенности некоторой ситуации, количественно равно начальной энтропии этой ситуации.

Но в общем случае неопределенность может быть снята только частично, поэтому количество информации (I), получаемой из некоторого сообщения, вычисляется как уменьшение энтропии, произошедшее в результате получения данного сообщения.

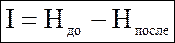
Для равновероятного случая, используя для расчета информации формулу Хартли, получим:

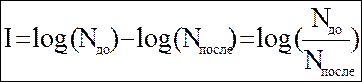
Как видно, второе равенство выводится на основании свойств логарифма. Таким образом, в равновероятном случае I зависит от того, во сколько раз изменилось количество вариантов выбора (рассматриваемое разнообразие).

Исходя из предыдущей формулы, можно сделать вывод, что при полном снятии неопределенности, когда N_после = 1:

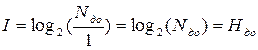
количество полученной в сообщении информации равно неопределенности, которая существовала до получения сообщения.

Если же N_после = N_до, то I = log₂(1) = 0, то это значит, что, неопределенность не изменилась, и, следовательно, информации получено не было.

Если N_после < N_до, то N_до / N_после > 1, или I > 0 (какая-то информация получена).

Если N_после > N_до, то N_до / N_после < 1, или I < 0 (информации нет).

Таким образом, количество полученной информации будет положительной величиной, если в результате получения сообщения количество рассматриваемых альтернатив уменьшилось, и отрицательной, - если оно увеличилось.

Если, например, количество рассматриваемых вариантов в результате получения сообщения уменьшилось вдвое, т. е. N_до / N_после = 2, то I = log₂(2) = 1 бит. Другими словами, получение 1 бита информации исключает из рассмотрения половину равнозначных вариантов.

В качестве примера можно рассмотреть опыт с колодой из 36 карт.

Допустим, кто-то выбирает одну карту из колоды. Нас интересует, какую именно из 36 карт он достал. Начальная неопределенность, рассчитываемая по формуле I = log₂(N_до / N_после), составляет:

I = log₂(36/1) = log₁₀(36) * 3,332 @ 5,17 бит.

Вытянувший карту сообщает нам часть информации. Используя формулу, определим, какое количество информации мы получаем из этих сообщений:

Вариант A. “Это карта красной масти”.

I = log₂(36/18) = log₂(2) = 1 бит (красных карт в колоде половина, поэтому неопределенность уменьшилась в 2 раза).

Вариант B. “Это карта пиковой масти”.

I = log₂(36/9) = log₂(4) = 2 бита (пиковые карты составляют четверть колоды, неопределенность уменьшилась в 4 раза).

Вариант С. “Это одна из старших карт: валет, дама, король или туз”.

I = log₂(36/16) = log₂(36) – log₂(16) = 5,17 – 4 = 1,17 бита (количество информации больше одного бита, т. к. неопределенность уменьшилась больше, чем в два раза).

Вариант D. “Это одна карта из колоды".

I = log₂(36/36) = log₂(1) = 0 бит (неопределенность не уменьшилась - сообщение не информативно).

Вариант E. “Это дама пик". I=log2(36/1)=log2(36)=5,17 бит (неопределенность полностью снята).

Дата добавления: 2014-01-05