
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторное и смешанное произведение векторов
|
|
|
|
Лекция 4
Результатом перемножения двух векторов может быть не только скаляр, но и вектор, который может умножаться на третий вектор.
Векторное произведение. Понятие векторного произведения, о котором пойдет речь в этом пункте, является объектом изучения теории трехмерного евклидова пространства. В евклидовом пространстве, число измерений которого отлично от трех, не имеется аналогий этого понятия.
Тройка векторов называется упорядоченной, если указано, какой из них считается первым, какой – вторым и какой – третьим. При записи тройки векторов мы всегда будем располагать эти векторы в порядке их следования (если для нас будет небезразличен порядок набора). Так, запись  ,
, 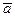 ,
, 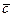 означает, что первым элементом тройки является вектор
означает, что первым элементом тройки является вектор  , вторым – вектор
, вторым – вектор 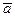 и третьим – вектор
и третьим – вектор 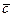 .
.
Упорядоченная тройка некомпланарных векторов 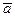 ,
,  ,
, 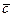 называется правой, если, находясь внутри трехгранного угла, образованного приведенными к общему началу векторами
называется правой, если, находясь внутри трехгранного угла, образованного приведенными к общему началу векторами 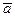 ,
,  ,
, 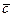 , мы видим кратчайший поворот от
, мы видим кратчайший поворот от 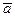 к
к  и от него к
и от него к 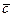 совершающимся против часовой стрелки. В противном случае тройка называется левой.
совершающимся против часовой стрелки. В противном случае тройка называется левой.
Удобное практическое правило определения правой тройки: упорядоченная тройка некомпланарных векторов 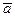 ,
,  ,
, 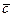 является правой, если после приведения к общему началу векторы располагаются так, как могут быть расположены соответственно большой, указательный и средний пальцы правой руки.
является правой, если после приведения к общему началу векторы располагаются так, как могут быть расположены соответственно большой, указательный и средний пальцы правой руки.
Векторным произведением вектора 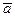 на вектор
на вектор  называется вектор
называется вектор 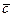 , обозначаемый символом
, обозначаемый символом  (или
(или  ) и удовлетворяющий следующим трем требованиям:
) и удовлетворяющий следующим трем требованиям:
1) длина вектора 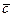 равна
равна 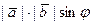 , где
, где 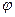 – угол между векторами
– угол между векторами 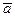 и
и  ;
;
2) вектор 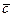 ортогонален плоскости векторов
ортогонален плоскости векторов 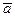 и
и  (
(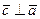 ,
,  );
);
3) векторы 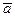 ,
,  ,
, 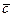 образуют правую тройку векторов.
образуют правую тройку векторов.
Требования 1 и 2 определяют вектор 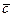 с точностью до двух взаимно противоположных направлений; требование 3 отбирает одно из этих двух направлений. В случае, когда
с точностью до двух взаимно противоположных направлений; требование 3 отбирает одно из этих двух направлений. В случае, когда 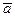 и
и  коллинеарные, тройка
коллинеарные, тройка 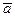 ,
,  ,
, 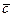 является компланарной, но в этом случае уже из требования 1 следует, что
является компланарной, но в этом случае уже из требования 1 следует, что  .
.
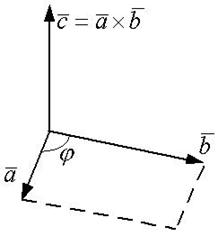
Рис. 4.1.
Понятие векторного произведения (так же, как и скалярное произведение) родилось в механике. Если вектор  изображает приложенную в некоторой точке
изображает приложенную в некоторой точке  силу, а вектор
силу, а вектор 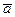 идет из некоторой точки
идет из некоторой точки 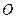 в точку
в точку  , то вектор
, то вектор 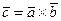 представляет собой момент силы
представляет собой момент силы  относительно точки
относительно точки 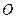 .
.
Свойства векторного произведения
1. 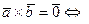 векторы
векторы 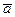 и
и  – коллинеарны.
– коллинеарны.
2. 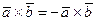 (антикоммутативность).
(антикоммутативность).
3.  ,
, 
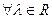 (однородность).
(однородность).
4.  ,
,
 (дистрибутивность).
(дистрибутивность).
Выражение векторного произведения через координаты сомножителей
Найдем векторные произведения базисных ортов 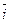 ,
, 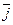 ,
,  . Результаты можно записать в следующую таблицу:
. Результаты можно записать в следующую таблицу:
Таблица 4.1
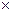
| 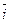
| 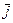
| 
|
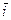
| 
| 
| 
|
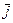
| 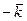
| 
| 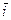
|

| 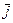
| 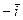
| 
|
Пользуясь этой таблицей и свойствами векторного произведения, найдем формулу для выражения векторного произведения через декартовы координаты сомножителей:

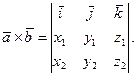
Пример 4.1. Найти векторное произведение векторов 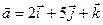 и
и 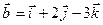 .
.
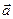 = (2, 5, 1);
= (2, 5, 1);  = (1, 2, -3)
= (1, 2, -3)
Решение.
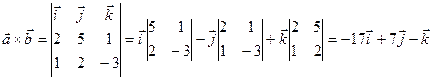 .
.
Пример 4.2. Найти площадь параллелограмма, построенного на векторах 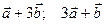 , если
, если 
Решение.

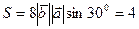 (ед2).
(ед2).
Пример 4.3. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3), С(0, 1, 0).
Решение.
Находим координаты векторов 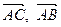 :
:
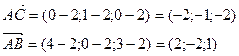
Площадь треугольника ABC равна половине площади параллелограмма, построенного на векторах  и
и  , поэтому находим векторное произведение этих векторов:
, поэтому находим векторное произведение этих векторов:


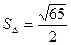 (ед2).
(ед2).
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 619; Нарушение авторских прав?; Мы поможем в написании вашей работы!