Уравнение линии в пространстве

Аналитическая геометрия в пространстве

Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению: .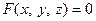

Это уравнение называется уравнением линии в пространстве.

Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким- либо уравнением.

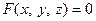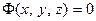Пусть и – уравнения поверхностей, пересекающихся по линии .

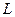Тогда пару уравнений

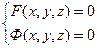
назовем уравнением линии в пространстве.

Уравнение прямой в пространстве по точке и направляющему вектору

Возьмем произвольную прямую и вектор , параллельный данной прямой. Вектор 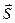называется направляющим вектором прямой.

На прямой возьмем две произвольные точк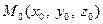и и .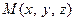

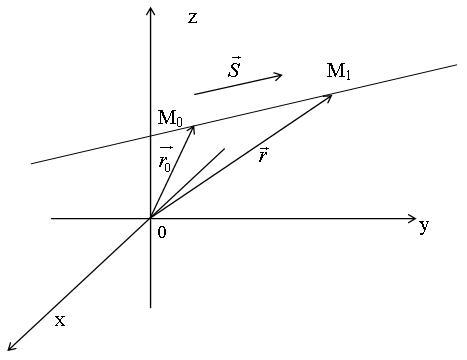
Рис. 6.1.

Обозначим радиус- векторы этих точек как 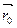и 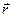, очевидно, что .

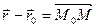Т.к. векторы 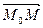и 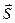коллинеарны, то верно соотношение 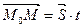, где t – некоторый параметр.

Итого, можно записать: .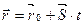

Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.

Это векторное уравнение может быть представлено в координатной форме:

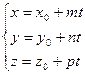
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:

.

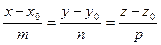Направляющими косинусами прямой называются направляющие косинусы вектора 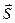, которые могут быть вычислены по формулам:

; .

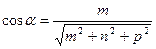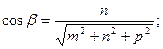
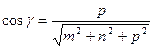Отсюда получим: .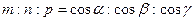

Числа m, n, p называются угловыми коэффициентами прямой. Т.к. 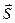- ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.

Уравнение прямой в пространстве, проходящей через две точки

Если на прямой в пространстве отметить две произвольные точк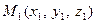и и 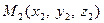, то координаты этих точек должны удовлетворять полученному выше уравнению прямой:

.

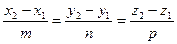Кроме того, для точки 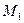можно записать:

.

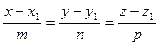Решая совместно эти уравнения, получим:

.

Это уравнение прямой, проходящей через две точки в пространстве.

Дата добавления: 2014-01-05