Структурные методы уменьшения влияния условий измерений на точность измерительных устройств

МЕТОДЫ И АЛГОРИТМЫ АДАПТАЦИИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ К ИЗМЕНЯЮЩИМСЯ ВНЕШНИМ УСЛОВИЯМ

В лекции 4 были подробно рассмотрены вопросы влияния различных внешних воздействий на точность измерений. К числу таких воздействий относятся как помехи и возмущения, так и изменяющиеся внешние условия проведения измерения.

Характер погрешности во многом определяется видом вызвавших его воздействий. Помехи и возмущения вызывают случайные погрешности, в то время как изменяющиеся внешние условия (изменение температуры, влажности, давления окружающей среды, изменения питающих напряжений, влияние внешних электрических и магнитных полей) вызывают переменные систематические погрешности. Поскольку значения изменяющихся внешних воздействий обычно неизвестны, то переменные систематические погрешности проявляют себя как случайные функции времени. В отличие от случайных погрешностей эти функции являются нестационарными случайными функциями величин, сравнительно медленно изменяющихся во времени.

Соответственно характеру погрешности выбираются методы их уменьшения. При постоянстве значений измерительной величины наиболее эффективным методом уменьшения случайной погрешности является усреднение результатов многократных наблюдений. Уменьшение случайной погрешности, когда измеряемая величина изменяется во времени, добиваются с помощью сложных процедур фильтрации, выбором оптимального алгоритма оценки результатов измерений.

Что касается переменных систематических погрешностей, то методы их уменьшения основаны на адаптации измерительных устройств к изменяющимся внешним условиям измерений с применением структурных способов стабилизации, методов компенсации и коррекции погрешностей, чему и посвящается настоящая глава.

В основе структурных методов уменьшения переменных систематических погрешностей лежит структурная или временная избыточность, используемая для реализации принципа инвариантности (многоканальности). Под инвариантностью понимают компенсацию возмущений, т.е. достижение полной или частичной независимости результата измерений от дестабилизирующего фактора. В инвариантных системах помимо основного канала ОК преобразования создается второй канал (рис. 8.1) – вспомогательный (ВК).

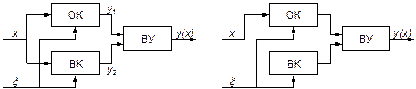а) б)

Рис. 8.1. Структуры инвариантных измерительных устройств:

а - измерительный сигнал и помеха на входе обоих каналов преобразования;

б - измерительный сигнал на входе одного канала преобразования

Отличие структуры инвариантной системы, построенной по схеме рис. 8.1, а от схемы по рис. 8.1, б сводится к тому, что в первом случае измеряемая величина x подводится к входу обоих каналов, во втором - только к входу основного канала. Возмущения x действуют на входы обоих каналов с соответствующими коэффициентами преобразования K₁ и K₂.

Для инвариантной системы по схеме рис.8.1, а функции преобразования каналов

y₁=F₁(x, x); y₂=F₂(x, x);

вычислительного устройства (ВУ) –

y=F (y₁, y₂)=y(х).

Для системы по схеме рис.8.1, б:

y₁=F₁(x, x); y₂=F₂(x); y=F (y₁, y₂)=y(х)

соответственно.

Если в системе по рис.8.1, а добиться равенства функций преобразования с коэффициентами передачи K₁=K₂=K по дестабилизирующему сигналу обоих каналов и инвертирования полезного сигнала во втором канале, то при условии линейности функции преобразования на выходе вычислительного устройства, работающего как сумматор, получим для первого варианта

y=F₁(x, x)+F₂(x, x)= K₁(x+x)+K₂(x-x)=(K₁+K₂)x=2Kx.

Для второго варианта (рис. 8.1, б)

y=F₁(x, x)+F₂(x)= K₁(x+x)+(-K₂x)=K₁x=Kx.

В обоих случаях влияние дестабилизирующего фактора отсутствует, а в первом - чувствительность к полезному сигналу удваивается. Если функции преобразования каналов нелинейны, то используют вычислительные устройства, производящие операции по более сложным алгоритмам.

Инвариантные системы могут иметь замкнутую структуру уравновешивающего действия, наиболее часто с отрицательной обратной связью.

Метод с отрицательной обратной связью является универсальным по отношению к различным видам дестабилизирующих факторов, так как уменьшается суммарный эффект их действия.

На рис. 8.2 показана структурная схема измерительной системы с обратной связью. Система имеет два канала преобразования: канал прямого преобразования КПП с коэффициентом передачи K_пп и канал обратного преобразования КОП с коэффициентом передачи K_оп. Каждый из каналов может реализоваться как одним (элементарным) преобразователем, так и сложным (в виде цепи преобразователей). Физическая величина на выходе КОП x_ос должна быть однородна с измеряемой величиной x.

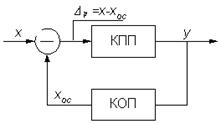Рис. 8.2 Структурная схема измерительной системы

с отрицательной обратной связью

Если функции преобразования каналов линейны, т.е.

y= K_ппx; x_ос= K_опy,

то при выборе обоих каналов в системе на входе канала прямого преобразования будет разностный сигнал D_p=x-x_ос и

y=K_ппD_p

Определим коэффициент передачи системы с отрицательной обратной связью:

,

откуда

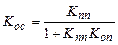. (8.1)

Функция преобразования системы

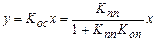. (8.2)

Как видно, добавление канала отрицательной обратной связи привело к уменьшению чувствительности в 1+K_ппK_оп раз.

Если принять K_ппK_оп>>1 (глубокая обратная связь), то получим

.

Это означает, что коэффициент передачи системы зависит только от коэффициента передачи канала обратного преобразования и не зависит от чувствительности канала прямого преобразования, и, следовательно, система становится нечувствительной к дестабилизирующим факторам, действующим на канал прямого преобразования.

Нестабильность в виде отклонения коэффициента передачи от номинальных значений вызывает мультипликативные погрешности

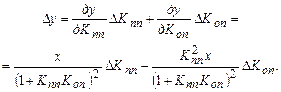. (8.3)

Разделив обе части на y, получим относительную погрешность

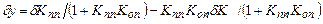, (8.4)

где 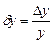; ; 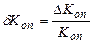- относительные погрешности системы с отрицательной обратной связью.

Погрешности dK_пп и dK_оп являются мультипликативными.

Уравнение (8.4) дает возможность количественно оценить влияние отрицательной обратной связи на повышение стабильности системы к внешним факторам. Исходная мультипликативная погрешность dK_пп уменьшается в (1+K_ппK_оп) раз, но добавляется погрешность dK_оп, создаваемая каналом обратного преобразования. При K_ппK_оп>>1 получим dy»d_оп. Это означает, что мультипликативную погрешность системы можно считать равной погрешности канала обратного преобразования. Поэтому метод применим, если имеется возможность выполнить высокоточный канал (чаще - это один преобразователь) отрицательной обратной связи.

Абсолютная аддитивная погрешность, связанная с параллельным смещением статической характеристики системы (из-за наличия порога срабатывания, дрейфа нуля и пр.), с введением отрицательной обратной связи практически не уменьшается, так как снижение коэффициента передачи системы в (1+K_ппK_оп) раз уменьшает не только погрешность, но и значение выходной величины.

При введении отрицательной обратной связи предполагается, что этим осуществляется статическое регулирование относительно влияющих величин. Этот процесс характеризуется коэффициентом статизма

. (8.5)

Уменьшение K_с неравномерно увеличивает стабильность системы. Наибольший эффект достигается при соотношении

(1-K_с)dK_пп / K_сK_пп» 3…5.

Дальнейшее уменьшение K_с незначительно уменьшает нестабильность системы, но ухудшает ее устойчивость как системы авторегулирования.

Расчет частотного коэффициента передачи (амплитудно-фазовой характеристики) системы с отрицательной обратной связью приводит к выражению, аналогичному (8.1), но в частотно-комплексном представлении:

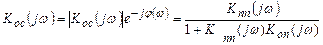, (8.6)

где K_пп(jw), K_оп(jw) - соответствующие частотные коэффициенты прямого канала и канала обратной связи.

При K_пп(jw)>1 можно получить приближенно

; .

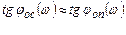Это означает, что введение отрицательной обратной связи подавляет изменение параметров прямого канала преобразований в диапазоне частот, полностью определяемом частотой пропускания канала отрицательной обратной связи. Анализ выражения (8.6) показывает также, что отрицательная обратная связь уменьшает нестабильность амплитудно-фазовой характеристики и влияние фазового сдвига.

К недостаткам метода отрицательной обратной связи следует отнести: необходимость избыточности канала прямого преобразования по чувствительности; возможность потери устойчивости системы при большом усилении в каналах; невозможность одновременного увеличения стабильности и расширения полосы частот.

Метод вспомогательных измерений заключается в том, что с помощью вспомогательных измерительных устройств ВИУ₁…ВИУ_n (рис.8.3) измеряются возмущающие воздействия x_1,…,x_n и производится расчет погрешности измерения по известной для основного средства измерений зависимости

Dy=F(x₁, x₂…x_n). (8.7)

Выходные сигналы ВИУ₁…ВИУ_n поступают на вычислительное устройство ВУ, которое вычисляет поправки Dy_п, необходимые для коррекции погрешности, согласно (8.7) и записанным в его память номинальным значением возмущающих факторов. В дальнейшем сигнал поправки Dy_п используется для коррекции выходного сигнала y основного средства измерений ОСИ.

Рис. 8.3. Структурная схема реализации метода вспомогательных измерений

Как видно на схеме (рис.8.3), на вычислительное устройство поступают сигналы, несущие информацию как о возмущениях x₁,…,x_l, поступающих на вход основного средства измерений вместе с полезным сигналом, так и о факторах x_l+1,…,x_n, характеризующих воздействие внешних условий измерения. Причем измерение и коррекция проводятся одновременно и непрерывно по различным каналам, благодаря чему рабочий диапазон частот корректируемого прибора не зависит от характеристик системы коррекции. Данное обстоятельство является основным достоинством метода.

К недостаткам метода следует отнести следующие: необходимость отдельного вспомогательного измерительного устройства для каждого фактора; возможность снижения влияния только легко учитываемых дестабилизирующих факторов и только при известной, независимой от времени зависимости погрешности СИ от этих факторов. Поэтому данный метод адаптации СИ к внешним условиям измерений применяется редко.

Итерационные методы [21,22] характеризуются тем, что в процессе измерения одного и того же значения измеряемой величины результат уточняется несколько раз и, в конечном счете, получается путем последовательных приближений. Метод требует избыточности средства измерений по быстродействию, а для своей реализации - структурной избыточности. Возможны реализации метода путем поочередного выполнения необходимых операций либо параллельным выполнением операций структурированной совокупностью дополнительных устройств. В первом случае выполняется временное разделение каналов, во втором - пространственное.

Рассмотрим метод итерации с временным разделением (рис.8.4).

Рис. 8.4. Структурная схема реализации итерационного метода

уменьшения погрешностей измерения (временное разделение)

С помощью средства измерений СИ при положении 1 переключателя П производится измерение входной величины, при положении 2 - измерение выходного сигнала x_оп точного обратного преобразователя ОП. Вычислительное устройство ВУ служит для запоминания результатов промежуточных измерений, для вычисления поправок и коррекции результатов. Обратный преобразователь ОП должен иметь линейную функцию преобразования x_оп=K_опy при обязательном соблюдении условия

,

где K_оп, K_си­ - коэффициенты передачи (номинальные значения) обратного преобразователя и средства измерений соответственно.

Итерационный алгоритм коррекции носит циклический характер и повторяется до достижения необходимой точности. Цикл начинается с измерения входной величины x (положение 1 переключателя П) и записи результата в память ВУ. Затем, после перевода переключателя П в положение 2, хранящийся в памяти сигнал поступает на вход обратного преобразователя, преобразуется в сигнал x_оп, измеряемый средствами измерений. Результат измерения поступает в ВУ, которое сравнивает его с результатом, записанным ранее в память, вычисляет значение поправки. Затем вновь измеряется x (П в положении 1) и в результат измерения вносится вычисленная поправка. Начинается новый цикл итерации. Итерационная процедура продолжается до достижения необходимой точности.

Рассмотрим, как проводится итерация, если функция преобразования имеет вид

y=K_си(1+d)x+D, (8.8)

где d - относительная мультипликативная погрешность; D - абсолютная аддитивная погрешность.

Результат первого измерения

y₀=K_си(1+d)x+D. (8.9)

Результат первого обратного преобразования

. (8.10)

После измерения сигнала x_оп1 на выходе ОП

y₁=K_сиx_оп1+D+K_сиdx_оп1=K_сиx(1+2d+d²)(2+d)D. (8.11)

Вычисления и запоминание в ВУ

Dy₁=y₁-y₀=D+K_сиdx+d(D+K_сиdx). (8.12)

После перевода П в положение 1результат измерения x

y₂=K_сиx+D+K_сиdx (8.13)

(предполагаем, что за время итераций D=const, K_сиd=const).

В результат измерения вводится первая поправка (первая итерация):

y₃=K_сиx+D+K_сиdx-Dy₁=K_сиx-d(D+ K_сиdx). (8.14)

Далее повторяется итерационная процедура.

Результат преобразования y₃

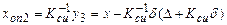. (8.15)

Результат измерения x_оп2:

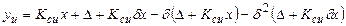. (8.16)

Вычисление поправки Dy₂ и запоминание:

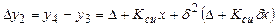. (8.17)

Новое измерение x и внесение второй поправки (вторая итерация):

. (8.18)

Поскольку d<1, то процесс итерации сходится. После n итераций получим результат:

. (8.19)

При d<1 , следовательно,

.

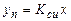Практически полной коррекции погрешности измерения добиться невозможно, так как будут оказывать влияние неточности средств, задействованных в итерационной процедуре.

Основным достоинством итерационных методов является корректирование общей погрешности СИ независимо от вызвавших ее причин.

Недостатки: ограниченная область применения из-за необходимости использования достаточно точного обратного преобразователя; необходимость оценки и учета погрешности дискретизации, связанной с периодическим отключением измеряемой величины.

При реализации итерационных методов с пространственным разделением каналов отключение измеряемой величины не требуется. На рис. 8.5 представлена структурная схема такой системы итеративной коррекции. В состав системы входит несколько одинаковых прямых (ПП) и обратных образцовых (ОП) преобразователей.

Преобразования, реализуемые системой:

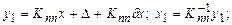
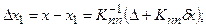
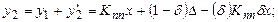
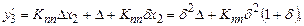
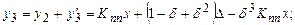
и т.д.

Рис. 8.5. Структурная схема реализации метода итеративной коррекции

погрешностей с пространственным разделением каналов

Поскольку d<<1, то y_n»K_ппx+D. Это означает, что мультипликативная погрешность скорректирована полностью, но остается аддитивная погрешность последнего преобразователя.

Методы образцовых мер (сигналов) основаны на определении в процессе цикла измерений реальных значений параметров функции преобразования средства измерений путем отключения от входа СИ измеряемой величины и подключения образцовых мер.

Метод предполагает, что функция преобразования средства измерений с достаточной точностью описывается полиномом порядка n-1.

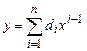, (8.20)

где d_i – коэффициенты функции преобразования средства измерений.

Структурная схема измерительной системы, реализующей данный метод, показана на рис. 8.6.

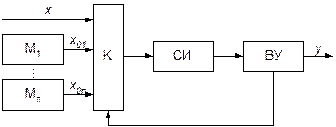Рис. 8.6. Структурная схема измерительной системы

с образцовыми сигналами

Дата добавления: 2014-01-05