Проверка нормальности результатов наблюдений

При числе результатов наблюдений <50 нормальность распределения проверяют при помощи составного критерия.

Критерий 1.

Вычисляют отношение :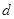

,

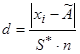где 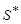– смещенная оценка среднеквадратического отклонения, которая вычисляется по формуле

.

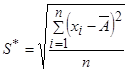Результаты наблюдений считаются нормально распределенными, если

<<,

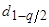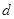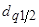где 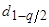и 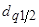- квантили распределения, получаемые из таблицы; 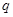– заранее выбранный уровень значимости.

Таблица

Статистика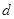

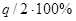
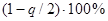
1%	5%	95%	99%
	0,9137	0,8884	0,7236	0,6829
	0,9001	0,8768	0,7304	0,6950
	0,8901	0,8686	0,7360	0,7040
	0,8826	0,8625	0,7404	0,7110
	0,8769	0,8578	0,7440	0,7167
	0,8722	0,8540	0,7470	0,7216
	0,8682	0,8508	0,7496	0,7256
	0,8648	0,8481	0,7518	0,7291

Критерий 2.

По этому критерию результаты наблюдений принадлежат нормальному распределению, если не более 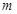разностей 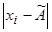превзошли значение , где определяется по формуле

,

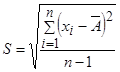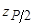– верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности .

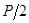Значения определяются из таблицы по выбранному уровню значимости 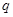и числу результатов наблюдений .

Если при проверке нормальности распределения для критерия 1 выбран уровень значимости , а для критерия 2 – , то результирующий уровень значимости составного критерия будет .

Распределение результатов наблюдений не соответствует нормальному в том случае, если не соблюдается хотя бы один из критериев.

Таблица

Значения для вычисления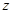

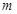
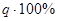
1%	2%	5%
		0,98	0,98	0,96
11 – 14		0,99	0,98	0,97
15 – 20		0,99	0,99	0,98
21 – 22		0,98	0,97	0,96
		0,98	0,98	0,96
24 – 27		0,98	0,98	0,97
28 – 32		0,99	0,98	0,97
33 – 35		0,99	0,98	0,98
36 – 49		0,99	0,99	0,98

Проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, следует проводить с уровнем значимости от 10 до 2%.

При большом числе наблюдений (более 50) используются критерий согласия К.Пирсона (критерий ) для группированных наблюдений и критерий Р.Мизеса – Н.В.Смирнова (критерий 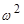) для негруппированных наблюдений.

Метод заключается в контроле отклонений гистограммы экспериментальных данных от гистограммы с таким же числом наблюдений, построенной на основе нормального распределения.

Порядок вычислений следующий:

1. Вычисляют среднее арифметическое результата измерений и оценку среднеквадратического результата наблюдений.

2. Группируют наблюдения по интервалам. Для каждого интервала вычисляют середину и подсчитывают эмпирическое число наблюдений 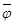, попавшее в каждый интервал. При числе наблюдений 40 – 100 принимают 5 – 9 интервалов.

3. Вычисляют теоретически соответствующее нормальному распределению число наблюдений для каждого интервала. Для этого из реальных середин интервалов переходят к нормированным :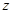

.

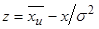Затем для каждого значения 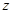находят значение функции плотности вероятностей :

.

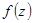4. Вычисляют ту часть общего числа имеющихся наблюдений, которая теоретически должна была быть в каждом из интервалов:

,

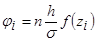где - общее число наблюдений; 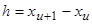- длина интервала, принятая при построении гистограммы.

5. Если в какой-либо интервал теоретически попадает меньше наблюдений, то его в обеих гистограммах соединяют с соседним интервалом.

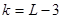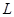6. Определяют число степеней свободы , где – общее число интервалов после укрупнения.

7. Вычисляют показатель разности частот :

,

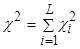где .

8. Выбирают уровень значимости (от 0,02≤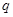≤0,1%). По уровню значимости и числу степеней свободы 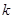находят границу критической области 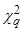. Если оказывается, что >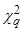, то гипотеза о нормальности отвергается.

Дата добавления: 2014-01-05