Пусть X — произвольное гладкое многообразие

Более точно можно ввести понятие динамической системы следующим образом

Динамической системой, заданной на гладком многообразии X, называется отображение вида g (t, x) = g^tx (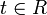 и ), которое является дифференцируемым отображением, причём g ⁰ — тождественное отображение пространства X и для любых s, 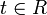выполняется тождество . Последнее означает, что { g^t } образует группу преобразований топологического пространства X.

Из дифференцируемости отображения g следует, что график функции g (t, x ₀) (при 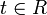) является дифференцируемой функцией времени и называется интегральной траекторией (кривой) динамической системы. Её проекция на пространство X, которое в таком случае носит название фазового пространства, называется фазовой траекторией (кривой) динамической системы.

Задание динамической системы, таким образом, эквивалентно разбиению фазового пространства на траектории.

Способы задания динамических систем

Для задания динамической системы необходимо описать её фазовое пространство X, множество моментов времени T и некоторое правило, описывающее движение точек фазового пространства со временем. Множество моментов времени T может быть как интервалом вещественной прямой (тогда говорят, что время непрерывно), так и множеством целых или натуральных чисел (дискретное время). Во втором случае «движение» точки фазового пространства больше напоминает мгновенные «скачки» из одной точки в другую: траектория такой системы является не гладкой кривой, а просто множеством точек, и называется обычно орбитой. Тем не менее, несмотря на внешнее различие, между системами с непрерывным и дискретным временем имеется тесная связь: многие свойства являются общими для этих классов систем или легко переносятся с одного на другой.

1. Дифференциальные уравнения

с параметрами

как математические модели

Во многих задачах естествознания возникают математические модели в виде автономных систем обыкновенных дифференциальных уравнений, зависящих от параметров. Такие уравнения описывают зависимость скорости изменений некото­рых величин, называемых фазовыми, или динамическими переменными, от значений самих этих величин. Фазовые переменные имеют самый разный смысл, определяемый природой изучаемого явления: это могут быть угол отклонения маятника от положения равновесия, концентрации химических веществ в реагирующей смеси, численности популяций животных и растений, составляющих экологическое сообщество, и т. п.

Кроме значений изучаемых величин, в правые части уравнений, как правило, входят коэффициенты или параметры, определяемые внутренними свойствами моделируемой системы или внешними условиями. Это могут быть длина маятника, ускорение свободного падения, константы скоростей химических реакций, скорость роста популяций и т. д. Величины такого рода, относительно которых предполагается постоянство во времени, мы будем называть параметрами модели.

2. Примеры моделей

Рассмотрим несколько примеров ма­тематических моделей из разных областей естествознания. Обратим внимание, что все эти модели нелинейны, содержат небольшое число (2—3) фазовых переменных и зависят от нескольких параметров. Далее мы используем данные модели для иллюстрации математических результатов, составляющих ос­новное содержание брошюры.

Пример 1. Химия. Один из традиционных объектов исследования в кинетике гетерогенного катализа — реакция окисления окиси углерода на платино­вом катализаторе. Для описания известных из экспериментов критических явлений в этой реакции, таких, как множественность стационарных состояний и автоколебания скорости реакции, был предложен следующий нелинейный кинетический механизм:

где Pt и PtCO — адсорбированные кислород и окись углерода, Pt — активный центр на поверхности платинового катализатора, (PtCO) — нереакционноспособная форма СО на поверхности ка­тализатора.

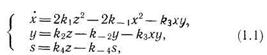
Схеме реакций 1—4 отвечает при условии постоянства температуры и концентрации веществ в газовой фазе следующая нестационарная кинетическая модель:

где 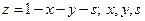— безразмерные концентрации

-константы скоростей соответствующих реакций (зависящие, в частности, от температуры и концентраций веществ в газовой фазе). Далее эти константы будут рассматриваться в качестве параметров

Таким образом, в рамках сделанных предположений реакция каталити­ческого окисления описывается системой трех дифференциальных уравнений, зависящей от семи параметров.

Пример 2. Экология. Классический объект экспериментальной и теоретиче­ской экологии — система двух популя­ций, взаимодействующих по принципу «хищник — жертва».

Рассмотрим модель динамики численности таких популяций, основанную на следующих предположениях:

1) популяция жертвы при малой численности размножается в геометрической прогрессии. Увеличение численности популяции приводит к конкуренции, в результате которой скорость размножения популяции линейно убывает с ростом ее численности. Это предположение дает классическую «логистическую» модель динамики численности изолированной популяции жертвы;

2) количество добываемой и потребляемой хищником в единицу времени пищи зависит от численности жертв При малой численности популяции жертвы эта зависимость прямо пропорциональная, при больших — наступает насыщение Потребленная пища с некоторым коэффициентом перерабатывается в биомассу хищников. Этот процесс включает в себя как рост, таки размножение хищников;

3) в отсутствие жертвы популяция хищника вымирает со скоростью, определяемой естественной смертностью и конкуренцией.

Сформулированные предпосылки, обоснованность и область применимо­сти которых мы здесь не обсуждаем, приводят к следующей модели*.

(1.2)

где х — численность популяции жертвы; у — численность популяции хищника; 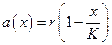— удельная скорость роста изолированной популяции жертвы; —трофическая функция хищника; 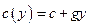— удельная скорость вымирания изолированной по­пуляции хищника.

Получаем систему двух дифференциальных уравнений, зависящую от семи параметров: .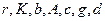

Замечание. Систему (1.2) можно рассматривать как обобщение классиче­ской модели Лотки — Вольтерры, в которой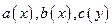—константы.

Пример 3. Иммунология. Рассмотрим модель динамики роста опухоли с учетом взаимодействия опухолевых кле­ток с двумя типами клеток, определяю­щих противоопухолевую резистентность организма*. Это клетки подсистемы естественной резистентности и клетки под­системы специфической противоопухоле­вой резистентности. Исходная модель,таким образом, включает три динамические переменные. Эту модель можно упростить, сохранив две динамические переменные — концентрации опухоле­вых клеток и клеток специфической реаистентности, а уровень активности подсистемы естественной резистентности включить в модель как параметр. Полученная модель в «безразмерных» переменных имеет вид:

Здесь х — концентрация свободных (не связанных с клетками-мишенями) клеток подсистемы специфической резистентности (эффекторных клеток), у — концентрация опухолевых клеток. В рамках модели учтены следующие процессы:

1) приток эффекторных клеток со скоростью ;

2) естественная гибель эффекторных клеток с относительной скоростью

3) гибель эффекторных и опухолевых клеток в результате их взаимодействия (члены, пропорциональные ху в обоих уравнениях);

4) наработка эффекторных клеток в результате дозревания предшественников. Скорость этого процесса зависит от концентрации опухолевых клеток и при их избытке достигает значения, равного ;

5) размножение опухолевых клеток. Учет действия системы неспецифической резистентности состоит в том, что удельная скорость размножения опухолевых клеток растет с ростом их концентрации, достигая некоторого максимального значения.

Таким образом, мы имеем систему двух дифференциальных уравнений, зависящую от шести параметров.

Дата добавления: 2014-01-05