Методы решения уравнения диффузии

Существует несколько методов решения уравнения (359). Рассмотрим лишь наиболее употребимые

Для решения уравнения диффузии вводится подстановка Больцмана:

(361)

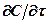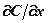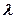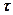Преобразовав выражения для и и дифференцируя по и 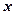, получим

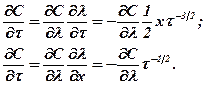
((362)

Выражение (359) приводится к виду

Подставив в это уравнение значения 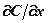и 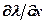из (362), найдем

Используя это выражение и уравнение (362), приходим к обыкновенному дифференциальному уравнению

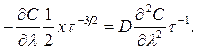
С учетом (361)

(363)

Пусть

(364)

где А, а, n — некоторые промежуточные константы. Подставив вы-
ражение (364) в (363), получим

(365)

Это уравнение выполняется при n=2, а=1/(4D). При этом (364)
принимает вид

(366)

Проинтегрировав (366) в пределах от до 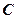и от О до 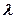, оп-
ределим

(368)

где — исходная концентрация источника диффузии.

Второе слагаемое в (368) называется функцией ошибок и обозначается через erf. Тогда выражение (368) запишется в виде

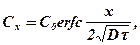(369)

где функцию erfc называют дополнительной функцией ошибок.

Значения функций и табулированы.

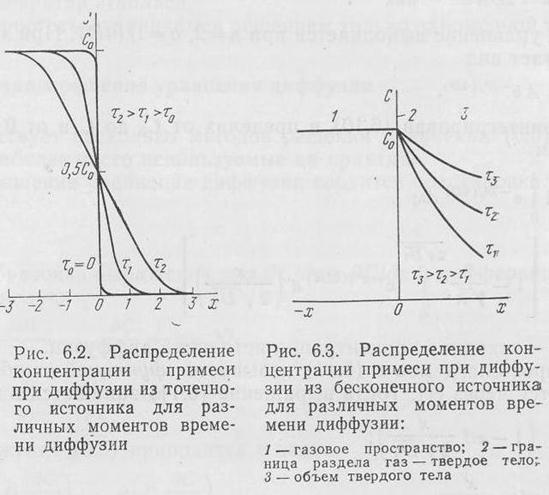
Формула (369) позволяет при известном значении коэффициента
диффузии вычислить распределение концентрации диффузанта
вдоль оси х для различных моментов времени (рис. Д.2). Если
диффузант распространяется в направлении х>0, то расчет проводится по правой ветви кривой, если в направлении х<0, то по левой.
Если диффузия протекает в обе стороны, то расчет ведется по всей
кривой.

На рис. Д.3 показано распределение концентрации диффузанта
при диффузии в заданную область (х>0) из источника с постоянной концентрацией . Соотношение (369) используется для рас-
чета диффузии заданного компонента в твердое тело, например полупроводник из газовой фазы постоянного состава (бесконечный
источник).

При диффузии из конечного источника его концентрация меняется, что приводит к изменению концентрации на границе раздела
источник — поверхность твердого тела. Процесс диффузии в этом
случае описывается уравнениями, подобными уравнениям распространения теплового импульса, а распределение концентрации диф-

фузанта— функцией Гаусса. Для одно-, двух- и трехмерной диффу-
зии получим

(370)

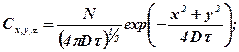(371)

(373)

где N — количество диффузанта (обычно твердого или жидкого).

Влияние температуры на коэффициент диффузии

Коэффициент диффузии D характеризует физические свойства
веществ, растворяемых друг в друге: основы А и диффузанта В.

Для газов коэффициент диффузии вычисляется по уравнению,
полученному нз кинетической теории газов:

(374)

где 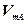, — молярные объемы компонентов А и В, М_A, M_B -
молярные массы компонентов А и В.

Для жидкостей - к
оэффициент диффузии для разбавленных растворов определяют
по уравнению Стокса — Эйнштейна:

(375) где — динамическая вязкость раствора; — постоянная Больц-
мана; — радиус молекул растворенного вещества.

Уравнение (375) неудобно для практического использования.
поэтому его приводят к виду

(376)

где F — параметр, зависящий от природы диффузанта и раствори-
теля.

При выводе и решении уравнений диффузии (357) и (359) атомная природа процесса не учитывалась. При ее учете необходимо рассмотривать кристаллическую решетку твердого
тела.

Каждый атом решетки совершает непрерывные колебания
около положения равновесия. За счет флуктуаций амплитуды не-
которые колебания могут оказаться настолько большими, что атомы
могут перейти на соседнюю плоскость кристаллической решетки.
Для этого необходимы большие флуктуации энергии и синхронность движения нескольких атомов. Установить
связь диффузии с беспорядочным движением атомов можно проанализи-
ровав две соседние атомные плоскости 1 и 2, находящиеся на рас-
стоянии а друг от друга, с концентрациями диффузанта в плоско-
стях, равными С₁ и С₂. Положив, что перемещения атомов из плоскости 1
на плоскость 2 и обратно равновероятны, а их частота одинакова.

Число атомов диффузанта на единице поверхности плоскости 1
, плоскости 2 .

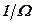За промежуток времени , малый по сравнению с , число
перемещающихся атомов диффузанта из плоскости 1 в плоскость 2
равно . Число плоскостей , в которые могут переместиться
атомы диффузанта, для разных кристаллических решеток различно.

Для простой кубической решетки .
В этом случае из всех атомов диффузанта, перемещающихся из
плоскости 1 в плоскость 2 за время , будет переходить только
1/6 часть. Результирующее число атомов на единицу поверхности,
переходящих из плоскости 1 в плоскость 2 в единицу времени, определяет поток атомов:

(377)

Если ось х перпендикулярно плоскостям 1, 2, то концентрации
С₁ и С₂ связаны между собой соотношением . С уче-
том этого уравнение (377) запишеться:

(378)

Сравнив (378) с (357), получим

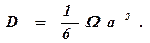(379)

Таким образом, коэффициент диффузии определяется частотой
перемещения атомов. Уравнение (379) является общим и не учитывает
механизма процесса. Для некубических и неидеальных решеток час-
тоты перемещения атомов с одной плоскости на другую не равны.
Поэтому коэффициенты диффузии для разных направлений различны.

Технологическими пара-
метрами, которые необходимо учитывать, являются: время диффузии, температура, растворимость примеси, свойства источника диф-
фузанта, состояние поверхности подложки, степень совершенства
кристаллической структуры подложки и др. Точность, с которой эти
параметры поддерживают в ТП, во многом определяет стабильность
качества диффузионных структур твердого тела
и соответствующих элементов ЭС.

Значение а в уравнении (379) зависит от вида кристаллической
решетки; оно незначительно меняется при изменении температуры.
Следовательно, существенная зависимость коэффициента диффузии
D от температуры Т, а также вида растворители и диффузанта оп-
ределяется частотой . Значение можно найти с
помощью расчета.

Рассмотрим атом внедрения в простой кубической решетке
(рис. Д.6, а). Атом совершает колебания во всех направлениях.
Его средняя частота колебаний в направлении х равна . Атомы
растворителя колеблются около своих положений равновесия. Большинство колебаний внедренного атома не приводит к изменению
его положения, однако отдельные, очень сильные колебания или не
которые случайные совпадения направлений колебаний внедренного атома и атомов растворителя могут привести к перемещению его
в соседнее положение. Расположение атомов в промежуточный
момент времени (в седловидной точке) показано на рис. Д.6, б. Для
вычисления определяют ту частоту колебаний в данном на-
правлении, которая приведет к перемещению атомов диффузанта:

(380)

где — изменение свободной энергии при перемещении атома.

3начение свободной энергии в зависимости от положения атома
внедрения представлено на рис. Д.6, в.

Число колебаний, приводящих к перемещению атомов в данном
направлении, определяется отношением энергии , к средней ки-
нетической энергии атомов в кристаллической решетке. При
повышении температуры средняя кинетическая энергия атомов воз-
растает. В результате отношение уменьшается и часто-
та растет.

Расположение атомов, показанное на рис. Д.6, б, возможно лишь
в течение короткого промежутка времени. Тем не менее. принято
считать, что уравнение (380) справедливо. Тогда

(381)

Подставив значенне в уравнение (379) и учтя, что , получим

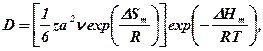(382)

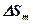где — энтальпия; — энтропия процесса.

Если уравнение (382) сравнить с эмпирическим

(383)

то нетрудно видеть, что коэффициент эквивалентен выражению,
заключенному в квадратные скобки в уравнении (382). При этом
— энергия, необходимая для перемещения атома из равновесного положения в промежуточное и называемая энергией ак-
тивации диффузии данной примеси.

Зависимость коэффициента диффузии от температуры в коорди-
натах прямолинейна.

Сильное влияние температуры на диффузионное распределение
вынуждает очень тщательно регулировать температуру при полу-
чении диффузионных слоев в производстве ЭС.

Влияние концентрации примесей на коэффициент диффузии

Зависимость коэффициента диффузии от концентрации диффу-
занта усложняет формулировку законов диффузии. Второй закон
Фика запишется в виде

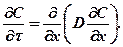(384)

Это более общая и в данном случае более удобная форма записи
второго закона Фика по сравнению с обычно используемой (359).

Подставив(361) в выражение (384), получим

(385)

При граничном условии для области х <0 С =1, а для об-
ласти х >0 С =0, производная 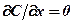при 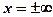. Решая (385),
найдем

(386)

После подстановки (в 386) коэффициент

(387)

Приняв время диффузии постоянным 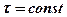и учитывая, что
получим

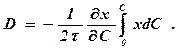(388)

Следовательно, для определения зависимости D от концентра - ции С необходимо найти значения 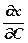и


Если коэффициент диффузии не
за
висит от концентрации, то диффузионная
граница на рис. Д.8 проходит через х =0 и граничная концентрация равна При
— наличии зависимости D от концентрации С характер кривой С(х) изменяется и диффу-
зионная граница смещается в положение 0₁.

Решение уравнения (388) осуществляют графическим способом по зависимости D от концентрации компонента.

т. е. для нахождения D в заданной точке А, необхо-димо
определить площадь заштрихованной
(рис. Д.8) фигуры, ограниченной диффузионной кривой в интервале концентраций от
0 до С_А, линией, соответствующей оконча-
тельной границе раздела, и осью х. Значе-
ние дх/дС графически можно найти, проведя к точке А касатель-
ную. Котангенс угла наклона этой прямой к оси абсцисс и являет-
ся искомой величиной. Подставив значения дх/дС и в (388),
получим значение D для данной точки.

Для двухкомпонентной системы коэффициент диффузии D свя-
зан с парциальными коэффициентами диффузии D₁ и D₂ соотноше-
нием

где С₁, С₂ — атомные концентрации компонентов 1 и 2.

Дата добавления: 2014-01-05